\definecolor{cb1}{RGB}{76,114,176} \definecolor{cb2}{RGB}{221,132,82} \definecolor{cb3}{RGB}{85,168,104} \definecolor{cb4}{RGB}{196,78,82} \definecolor{cb5}{RGB}{129,114,179} \definecolor{cb6}{RGB}{147,120,96} \definecolor{cb7}{RGB}{218,139,195} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \DeclareMathOperator{\bigO}{\mathcal O} \newcommand{\cH}{\mathcal{H}} \newcommand{\cX}{\mathcal{X}} \DeclareMathOperator{\Cov}{Cov} \DeclareMathOperator{\E}{\mathbb{E}} \newcommand{\HS}{\mathrm{HS}} \DeclareMathOperator{\HSIC}{HSIC} \DeclareMathOperator{\mean}{mean} \DeclareMathOperator{\MMD}{MMD} \DeclareMathOperator{\MMDhat}{\widehat{MMD}} \newcommand{\R}{\mathbb{R}} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\span}{span} \newcommand{\tp}{^\mathsf{T}} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Var}{Var} \newcommand{\indep}{{\perp\!\!\!\perp}} \newcommand{\cP}[1]{{\color{cb1} #1}} \newcommand{\PP}{\cP{\mathbb{P}}} \newcommand{\pp}{\cP{p}} \newcommand{\X}{\cP{X}} \newcommand{\Xi}{\cP{X_i}} \newcommand{\Xp}{\cP{X'}} \newcommand{\Xpp}{\cP{X''}} \newcommand{\Hx}{\cP{\cH_x}} \newcommand{\kx}{\cP{k_x}} \newcommand{\fc}{\cP{f}} \newcommand{\muP}{\cP{\mu_{\mathbb P}}} \newcommand{\Pdata}{\cP{\mathbb{P}_\mathrm{data}}} \newcommand{\cQ}[1]{{\color{cb2} #1}} \newcommand{\QQ}{\cQ{\mathbb{Q}}} \newcommand{\qq}{\cQ{q}} \newcommand{\qtheta}{\cQ{q_\theta}} \newcommand{\Y}{\cQ{Y}} \newcommand{\Yp}{\cQ{Y'}} \newcommand{\Ypp}{\cQ{Y''}} \newcommand{\Yj}{\cQ{Y_j}} \newcommand{\thetac}{\cQ{\theta}} \newcommand{\vtheta}{\thetac} \newcommand{\Qtheta}{\QQ_\thetac} \newcommand{\Gtheta}{\cQ{G_\theta}} \newcommand{\Hy}{\cQ{\cH_y}} \newcommand{\ky}{\cQ{k_y}} \newcommand{\gc}{\cQ{g}} \newcommand{\muQ}{\cQ{\mu_{\mathbb Q}}} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\Norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\hnorm}[2][\cH]{\norm{#2}_{#1}} \newcommand{\hNorm}[2][\cH]{\Norm{#2}_{#1}} \newcommand{\inner}[2]{\langle #1, #2 \rangle} \newcommand{\Inner}[2]{\left\langle #1, #2 \right\rangle} \newcommand{\hinner}[3][\cH]{\inner{#2}{#3}_{#1}} \newcommand{\hInner}[3][\cH]{\Inner{#2}{#3}_{#1}} \newcommand{\cpsi}[1]{{\color{cb3} #1}} \newcommand{\psic}{\cpsi{\psi}} \newcommand{\Psic}{\cpsi{\Psi}} \newcommand{\Dpsi}{\cpsi{D_\psi}}

(Deep) Kernel Mean Embeddings
for Representing and Learning on Distributions

Danica J. Sutherland(she/her)
University of British Columbia + Amii
Lifting Inference with Kernel Embeddings (LIKE-23), June 2023

This talk: how to lift inference with kernel embeddings

Slides at djsutherland.ml/slides/like23

(Swipe or arrow keys to move through slides; m for a menu to jump; ? for more.)
PDF version at djsutherland.ml/slides/like23.pdf

HTML version at djsutherland.ml/slides/like23

Part I: Kernels

Why kernels?

  • Machine learning! …but how do we actually do it?
  • Linear models! f(x) = w_0 + w x , \hat{y}(x) = \sign(f(x))
  • Extend x … f(x) = w\tp (1, x, x^2) = w\tp \phi(x)
  • Kernels are basically a way to study doing this
    with any, potentially very complicated, \phi
  • Convenient way to make models on documents, graphs, videos, datasets, probability distributions, …
  • \phi will live in a reproducing kernel Hilbert space
2022-10-03T18:52:53.597624 image/svg+xml Matplotlib v3.5.1, https://matplotlib.org/

Hilbert spaces

  • A complete (real or complex) inner product space
  • Inner product space: a vector space with an inner product:
    • \hinner{\alpha_1 f_1 + \alpha_2 f_2}{g} = \alpha_1 \hinner{f_1}{g} + \alpha_2 \hinner{f_2}{g}
    • \hinner{f}{g} = \hinner{g}{f}
    • \hinner{f}{f} > 0 for f \ne 0 , \hinner{0}{0} = 0
    Induces a norm: \hnorm f = \sqrt{\hinner{f}{f}}
  • Complete: “well-behaved” (Cauchy sequences have limits in \cH )

Kernel: an inner product between feature maps

  • Call our domain \cX , some set
    • \R^d , functions, distributions of graphs of images, …
  • k : \cX \times \cX \to \R is a kernel on \cX if there exists a Hilbert space \cH and a feature map \phi : \cX \to \cH so that k(x, y) = \hinner{\phi(x)}{\phi(y)}
  • Roughly, k is a notion of “similarity” between inputs
  • Linear kernel on \R^d : k(x, y) = \hinner[\R^d]{x}{y}

Aside: the name “kernel”

  • Our concept: "positive semi-definite kernel," "Mercer kernel," "RKHS kernel"
  • Exactly the same: GP covariance function
  • Semi-related: kernel density estimation
    • k : \cX \times \cX \to \R , usually symmetric, like RKHS kernel
    • Always requires \int k(x, y) \mathrm d y = 1 , unlike RKHS kernel
    • Often requires k(x, y) \ge 0 , unlike RKHS kernel
    • Not required to be inner product, unlike RKHS kernel
  • Unrelated:
    • The kernel (null space) of a linear map
    • The kernel of a probability density
    • The kernel of a convolution
    • CUDA kernels
    • The Linux kernel
    • Popcorn kernels

Building kernels from other kernels

  • Scaling: if \gamma \ge 0 , k_\gamma(x, y) = \gamma k(x, y) is a kernel
    • k_\gamma(x, y) = \gamma \hinner{\phi(x)}{\phi(y)} = \hinner{\sqrt\gamma \phi(x)}{\sqrt\gamma \phi(y)}
  • Sum: k_+(x, y) = k_1(x, y) + k_2(x, y) is a kernel
    • k_+(x, y) = \hInner[\cH_1 \oplus \cH_2]{\begin{bmatrix}\phi_1(x) \\ \phi_2(x)\end{bmatrix}}{\begin{bmatrix}\phi_1(y) \\ \phi_2(y)\end{bmatrix}}
  • Is k_1(x, y) - k_2(x, y) necessarily a kernel?
    • Take k_1(x, y) = 0 , k_2(x, y) = x y , x \ne 0 .
    • Then k_1(x, x) - k_2(x, x) = - x^2 < 0
    • But k(x, x) = \hnorm{\phi(x)}^2 \ge 0 .

Positive definiteness

  • A symmetric function k : \cX \times \cX \to \R i.e. k(x, y) = k(y, x)
    is positive semi-definite
    if for all n \ge 1 , (a_1, \dots, a_n) \in \R^n , (x_1, \dots, x_n) \in \cX^n , \sum_{i=1}^n \sum_{j=1}^n a_i a_j k(x_i, x_j) \ge 0
  • Equivalent: n \times n kernel matrix K is psd (eigenvalues \ge 0 ) K := \begin{bmatrix} k(x_1, x_1) & k(x_1, x_2) & \dots & k(x_1, x_n) \\ k(x_2, x_1) & k(x_2, x_2) & \dots & k(x_2, x_n) \\ \vdots & \vdots & \ddots & \vdots \\ k(x_n, x_1) & k(x_n, x_2) & \dots & k(x_n, x_n) \end{bmatrix}
  • Hilbert space kernels are psd
    \begin{align*} \!\!\!\! \sum_{i=1}^n \sum_{j=1}^n \hinner{a_i \phi(x_i)}{a_j \phi(x_j)} &\fragment[3]{{}= \hInner{\sum_{i=1}^n a_i \phi(x_i)}{\sum_{j=1}^n a_j \phi(x_j)}} \\&\fragment[4]{{}= \hNorm{ \sum_{i=1}^n a_i \phi(x_i) }^2} \fragment[5]{{}\ge 0} \end{align*}
  • psd functions are Hilbert space kernels
    • Moore-Aronszajn Theorem; we'll come back to this

Some more ways to build kernels

  • Limits: if k_\infty(x, y) = \lim_{m \to \infty} k_m(x, y) exists, k_\infty is psd
    • \displaystyle \lim_{m\to\infty} \sum_{i=1}^n \sum_{j=1}^n a_i a_j k_m(x_i, x_j) \ge 0
  • Products: k_\times(x, y) = k_1(x, y) k_2(x, y) is psd
    • Let V \sim \mathcal N(0, K_1) , W \sim \mathcal N(0, K_2) be independent
    • \Cov(V_i W_i, V_j W_j) = \Cov(V_i, V_j) \Cov(W_i, W_j) = k_\times(x_i, x_j)
    • Covariance matrices are psd, so k_\times is too
  • Powers: k_n(x, y) = k(x, y)^n is pd for any integer n \ge 0

    \fragment[ 8 ]{\big(} x \tp y \fragment[ 7 ]{ {} + c } \fragment[ 8 ]{\big)}\fragment[ 8 ]{^n} , the polynomial kernel

  • Exponents: k_{\exp}(x, y) = \exp(k(x, y)) is pd
    • k_{\exp}(x, y) = \lim_{N \to \infty} \sum_{n=0}^N \frac{1}{n!} k(x, y)^n
  • If f : \X \to \R , k_f(x, y) = f(x) k(x, y) f(y) is pd
    • Use the feature map x \mapsto f(x) \phi(x)

\fragment[ 20 ]{\exp\Big( -\frac{1}{2 \sigma^2} \norm{x}^2 \Big)} \fragment[ 19 ]{\exp\Big(} \fragment[ 18 ]{\frac{1}{\sigma^2}} x\tp y \fragment[ 19 ]{\Big)} \fragment[ 20 ]{\exp\Big( -\frac{1}{2 \sigma^2} \norm{y}^2 \Big)}

{} = \exp\Big( - \frac{1}{2 \sigma^2} \left[ \norm{x}^2 - 2 x\tp y + \norm{y}^2 \right] \Big)

{} = \exp\Big( - \frac{\norm{x - y}^2}{2 \sigma^2} \Big) , the Gaussian kernel

Reproducing property

  • Recall original motivating example with \cX = \R \qquad \phi(x) = (1, x, x^2) \in \R^3
  • Kernel is k(x, y) = \hinner{\phi(x)}{\phi(y)} = 1 + x y + x^2 y^2
  • Classifier based on linear f(x) = \hinner{w}{\phi(x)}
  • f(\cdot) is the function f itself; corresponds to vector w in \R^3
    f(x) \in \R is the function evaluated at a point x
  • Elements of \cH are functions, f : \cX \to \R
  • Reproducing property: f(x) = \hinner{f(\cdot)}{\phi(x)} for f \in \cH
2022-03-06T21:53:16.613121 image/svg+xml Matplotlib v3.5.1, https://matplotlib.org/

Reproducing kernel Hilbert space (RKHS)

  • Every psd kernel k on \cX defines a (unique) Hilbert space, its RKHS \cH ,
    and a map \phi : \cX \to \cH where
    • k(x, y) = \hinner{\phi(x)}{\phi(y)}
    • Elements f \in \cH are functions on \cX , with f(x) = \hinner{f}{\phi(x)}
  • Combining the two, we sometimes write k(x, \cdot) = \phi(x)
  • k(x, \cdot) is the evaluation functional
    An RKHS is defined by it being continuous, or \abs{f(x)} \le M_x \hnorm{f}

Moore-Aronszajn Theorem

  • Building \cH for a given psd k :
    • Start with \cH_0 = \span\left(\left\{ k(x, \cdot) : x \in \cX \right\}\right)
    • Define \hinner[\cH_0]{\cdot}{\cdot} from \hinner[\cH_0]{k(x,\cdot)}{k(y,\cdot)} = k(x, y)
    • Take \cH to be completion of \cH_0 in the metric from \hinner[\cH_0]{\cdot}{\cdot}
    • Get that the reproducing property holds for k(x, \cdot) in \cH
    • Can also show uniqueness
  • Theorem: k is psd iff it's the reproducing kernel of an RKHS

A quick check: linear kernels

  • k(x, y) = x\tp y on \cX = \R^d
    • k(x, \cdot) = [y \mapsto x\tp y] “corresponds to” x
  • If \displaystyle f(y) = \sum_{i=1}^n a_i k(x_i, y) , then f(y) = \left[ \sum_{i=1}^n a_i x_i \right]\tp y
  • Closure doesn't add anything here, since \R^d is closed
  • So, linear kernel gives you RKHS of linear functions
  • \hnorm{f} = \sqrt{\sum_{i=1}^n \sum_{j=1}^n a_i a_j k(x_i, x_j)} = \Norm{\sum_{i=1}^n a_i x_i}

More complicated: Gaussian kernels

k(x, y) = \exp(\frac{1}{2 \sigma^2} \norm{x - y}^2)

  • \cH is infinite-dimensional
  • Functions in \cH are bounded: f(x) = \hinner{f}{k(x, \cdot)} \le \sqrt{k(x, x)} \hnorm{f} = \hnorm{f}
  • Choice of \sigma controls how fast functions can vary: \begin{align*} f(x + t) - f(x) &\le \hnorm{k(x + t, \cdot) - k(x', \cdot)} \hnorm{f} \\ \hnorm{k(x + t, \cdot) - k(x, \cdot)}^2 & = 2 - 2 k(x, x + t) = 2 - 2 \exp\left(-\tfrac{\norm{t}^2}{2 \sigma^2}\right) \end{align*}
  • Can say lots more with Fourier properties
2023-06-25T23:35:05.240018 image/svg+xml Matplotlib v3.7.1, https://matplotlib.org/

Kernel ridge regression

\hat f = \argmin_{f \in \cH} \frac1n \sum_{i=1}^n ( f(x_i) - y_i )^2 + \lambda \hnorm{f}^2

Linear kernel gives normal ridge regression: \qquad\qquad % ??? \hat f(x) = \hat w\tp x; \quad \hat w = \argmin_{w \in \R^d} \frac1n \sum_{i=1}^n ( w\tp x_i - y_i )^2 + \lambda \norm{w}^2 Nonlinear kernels will give nonlinear regression!

How to find \hat f ? Representer Theorem: \hat f = \sum_{i=1}^n \hat\alpha_i k(x_i, \cdot)

  • Let \cH_X = \span\{ k(x_i, \cdot) \}_{i=1}^n , and \cH_\perp its orthogonal complement in \cH
  • Decompose f = f_X + f_\perp with f_X \in \cH_X , f_\perp \in \cH_\perp
  • f(x_i) = \hinner{f_X + f_\perp}{k(x_i, \cdot)} = \hinner{f_X}{k(x_i, \cdot)}
  • \hnorm{f}^2 = \hnorm{f_X}^2 + \hnorm{f_\perp}^2
  • Minimizer needs f_\perp = 0 , and so \hat f = \sum_{i=1}^n \alpha_i k(x_i, \cdot)

\begin{align*} \sum_{i=1}^n \left( \sum_{j=1}^n \alpha_j k(x_i, x_j) - y_i \right)^2 &= \sum_{i=1}^n \left( [K \alpha]_i - y_i \right)^2 \fragment[11]{{}= \norm{K \alpha - y}^2} \\&\fragment[12]{{} = \alpha\tp K^2 \alpha - 2 y \tp K \alpha + y\tp y} \end{align*}

\hNorm{\sum_{i=1}^n \alpha_i k(x_i, \cdot)}^2 = \sum_{i=1}^n \sum_{j=1}^n \alpha_i k(x_i, x_j) \alpha_j \fragment[16]{{} = \alpha\tp K \alpha}

\begin{align*} \hat\alpha &= \argmin_{\alpha \in \R^n} \alpha\tp K^2 \alpha - 2 y \tp K \alpha + y\tp y + n \lambda \alpha\tp K \alpha \\&\fragment[21]{{} = \argmin_{\alpha \in \R^n} \alpha\tp K (K + n \lambda I) \alpha - 2 y \tp K \alpha} \end{align*}

Setting derivative to zero gives K (K + n \lambda I) \hat\alpha = K y ,
satisfied by \hat\alpha = (K + n \lambda I)^{-1} y

Kernel ridge regression and GP regression

  • Compare to regression with \mathcal{GP}(0, k) prior, \mathcal N(0, \sigma^2) observation noise
  • If we take \lambda = \sigma^2 / n , KRR is exactly the GP regression posterior mean
  • Note that GP posterior samples are not in \cH , but are in a slightly bigger RKHS
  • Also a connection between posterior variance and KRR worst-case error
  • For many more details:

Other kernel algorithms

  • Representer theorem applies if R is strictly increasing in \min_{f \in \cH} L(f(x_1), \cdots, f(x_n)) + R(\hnorm{f})
  • Kernel methods can then train based on kernel matrix K
  • Classification algorithms:
    • Support vector machines: L is hinge loss
    • Kernel logistic regression: L is logistic loss
  • Principal component analysis, canonical correlation analysis
  • Many, many more…
  • But not everything works...e.g. Lasso \norm w_1 regularizer

Some very very quick theory

  • Generalization: how close is my training set error to the population error?
    • Say k(x, x) \le 1 , consider \{ f \in \cH : \hnorm f \le B \} , \rho -Lipschitz loss
    • Rademacher argument implies expected overfitting \le \frac{2 \rho B}{\sqrt n}
    • If “truth” has low RKHS norm, can learn efficiently
  • Approximation: how big is RKHS norm of target function?
    • For universal kernels, can approximate any target with finite norm
    • Gaussian is universal 💪 (nothing finite-dimensional can be)
    • But “finite” can be really really really big

Limitations of kernel-based learning

  • Generally bad at learning sparsity
    • e.g. f(x_1, \dots, x_d) = 3 x_2 - 5 x_{17} for large d
  • Provably statistically slower than deep learning for a few problems
    • e.g. to learn a single ReLU, \max(0, w\tp x) , need norm exponential in d [Yehudai/Shamir NeurIPS-19]
    • Also some hierarchical problems, etc [Kamath+ COLT-20]
    • Generally apply to learning with any fixed kernel
  • \bigO(n^3) computational complexity, \bigO(n^2) memory
    • Various approximations you can make

Part II: (Deep) Kernel Mean Embeddings

Mean embeddings of distributions

  • Represent point x \in \cX as k(x, \cdot) : \quad f(x) = \hinner{f}{k(x, \cdot)}
  • Represent distribution \PP as \muP : \quad \E_{X \sim \PP} f(X) = \hinner{f}{\muP} \E_{\X \sim \PP} f(\X) = \E_{\X \sim \PP} \hinner{f}{k(\X, \cdot)} \fragment{{}= \hinner{f}{ \underbrace{\E_{\X \sim \PP} k(\X, \cdot)}_{\muP} }}
    • Last step assumed \E \sqrt{k(\X, \X)} < \infty (Bochner integrability)
  • \hinner{\muP}{\muQ} = \E_{\X \sim \PP, \Y \sim \QQ} k(\X, \Y)
  • Okay. Why?
    • One reason: ML on distributions [Szabó+ JMLR-16]
    • More common reason: comparing distributions

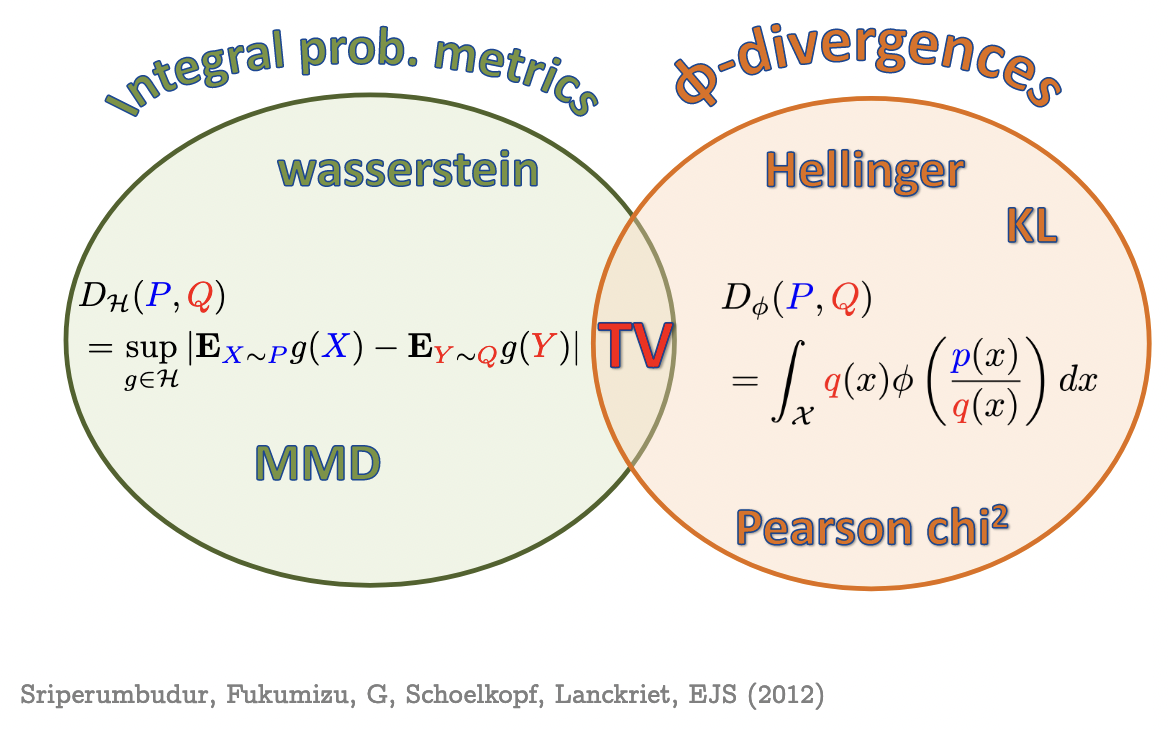
Maximum Mean Discrepancy

\begin{align*} \MMD(\PP, \QQ) &= \hnorm{\muP - \muQ} \\&\fragment[0]{= \sup_{\hnorm{f} \le 1} \hinner{f}{\muP - \muQ}} \\&\fragment[1]{= \sup_{\hnorm{f} \le 1} \E_{X \sim \PP} f(X) - \E_{Y \sim \QQ} f(Y)} \end{align*}

  • Last line is Integral Probability Metric (IPM) form
  • f is called “witness function” or “critic”: high on \PP , low on \QQ f^*(t) \propto \hinner{\muP - \muQ}{k(t, \cdot)} = \E_\PP k(t, X) - \E_\QQ k(t, Y)
2023-06-26T00:47:55.423729 image/svg+xml Matplotlib v3.7.1, https://matplotlib.org/

MMD properties

\MMD(\PP, \QQ) = \hnorm{\muP - \muQ}

  • \MMD(\PP, \PP) = 0 , symmetry, triangle inequality
  • If k is characteristic, then \MMD(\PP, \QQ) = 0 iff \PP = \QQ
    • i.e. \PP \mapsto \muP is injective
    • Makes MMD a metric on probability distributions
    • Universal \implies characteristic
  • If we use a linear kernel:
    • \MMD(\PP, \QQ) = \hnorm{\muP - \muQ} just Euclidean distance between means
  • If we use k(x, y) = d(x, 0) + d(y, 0) - d(x, y) ,
    the squared MMD becomes the energy distance [Sejdinovic+ Annals-13]

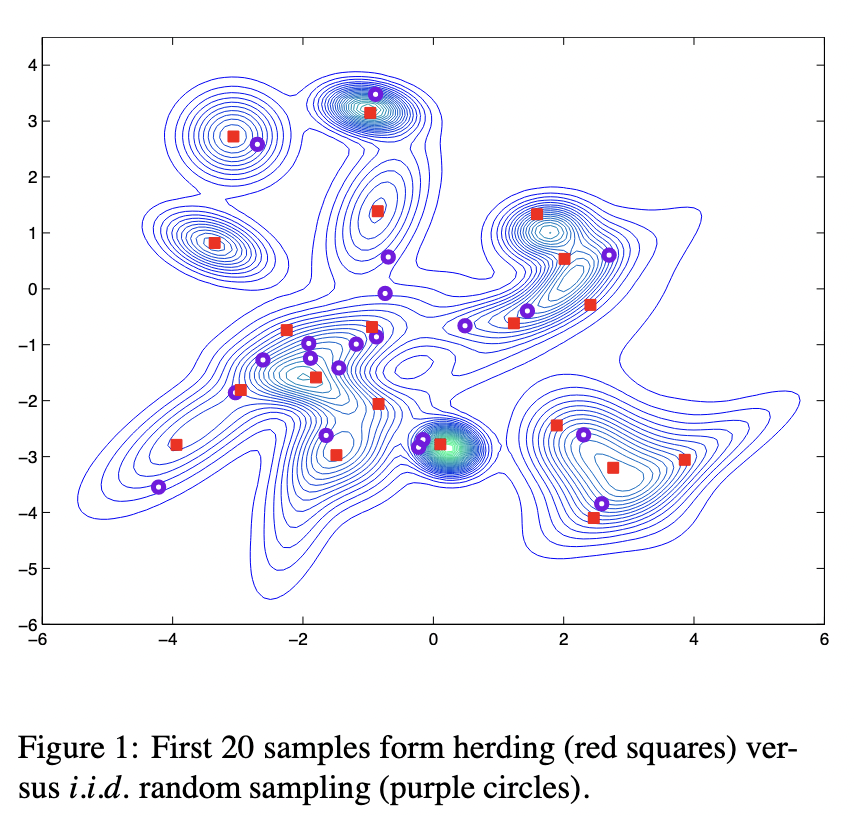
Application: Kernel Herding

  • Want a "super-sample" from \PP : \E f(\X) \approx \frac1n \sum_j f(\Yj) for all f
    • Letting \QQ = \frac1T \sum_{j=1}^T \delta_{\Yj} , want \hinner{f}{\muQ} \approx \hinner{f}{\muP} for all f \in \cH
    • Error \le \hnorm f \MMD(\PP, \QQ)
  • Greedily minimize the MMD: \Y_{\cQ{T+1}} \in \argmin_{\Y \in \cX} \E_{\Xp \sim \PP} k(\Y, \Xp) - \frac{1}{T+1} \sum_{j=1}^T k(\Y, \Yj)
  • Get \bigO(1 / T) approximation instead of \bigO(1 / \sqrt T) with random samples

Estimating MMD from samples

\begin{align*} \MMD_k^2(\PP, \QQ) &= \hinner{\muP}{\muP} - 2 \hinner{\muP}{\muQ} + \hinner{\muQ}{\muQ} \\&\fragment[0]{ {} = \E_{\substack{\X, \Xp \sim \PP\\\Y, \Yp \sim \QQ}}\left[ k(\X, \Xp) - 2 k(\X, \Y) + k(\Y, \Yp) \right] } \\ \fragment[1]{ \MMDhat_k^2(\X, \Y) } & \fragment[1]{{} = \fragment[2][highlight-current-red]{\mean(K_{\X\X})} + \fragment[3][highlight-current-red]{\mean(K_{\Y\Y})} - 2 \fragment[4][highlight-current-red]{\mean(K_{\X\Y})} } \end{align*}

K_{\X\X}

1.00.20.6
0.21.00.5
0.60.51.0

K_{\Y\Y}

1.00.80.7
0.81.00.6
0.70.61.0

K_{\X\Y}

0.30.10.2
0.20.30.3
0.20.10.4

MMD vs other distances

  • MMD has easy \bigO(n^2) estimator
    • block or incomplete estimators are \bigO(n^\alpha) for \alpha \in [1, 2] , but noisier
  • For bounded kernel, \bigO_p(1 / \sqrt n) estimation error
    • Independent of data dimension!
    • But, no free lunch…the value of the MMD generally shrinks with growing dimension, so constant \bigO_p(1 / \sqrt n) error gets worse relatively

GP view of MMD

\begin{align*} \MMD^2(\PP, \QQ) &= \left( \sup_{f : \hnorm f \le 1} \E_{\X \sim \PP} f(\X) - \E_{Y \sim \QQ} f(\Y) \right)^2 \\&= \Var_{f \sim \mathcal{GP}(0, k)}\left[ \E_{\X \sim \PP} f(\X) - \E_{Y \sim \QQ} f(\Y) \right] \end{align*}

Application: Two-sample testing

  • Given samples from two unknown distributions \X \sim \PP \qquad \Y \sim \QQ
  • Question: is \PP = \QQ ?
  • Hypothesis testing approach: H_0: \PP = \QQ \qquad H_1: \PP \ne \QQ
  • Reject H_0 if \MMDhat(\X, \Y) > c_\alpha
  • Do smokers/non-smokers get different cancers?
  • Do Brits have the same friend network types as Americans?
  • When does my laser agree with the one on Mars?
  • Are storms in the 2000s different from storms in the 1800s?
  • Does presence of this protein affect DNA binding? [MMDiff2]
  • Do these dob and birthday columns mean the same thing?
  • Does my generative model \Qtheta match \Pdata ?

What's a hypothesis test again?

2022-10-03T21:54:51.737361 image/svg+xml Matplotlib v3.5.1, https://matplotlib.org/

MMD-based testing

  • H_0 : n \MMDhat^2 converges in distribution to…something
    • Infinite mixture of \chi^2 s, params depend on \PP and k
    • Can estimate threshold with permutation testing
  • H_1 : \sqrt n (\MMDhat^2 - \MMD^2) \stackrel{d}{\to} asymptotically normal
  • Any characteristic kernel gives consistent test…eventually
  • Need enormous n if kernel is bad for problem

Classifier two-sample tests

  • \hat T(\X, \Y) is the accuracy of f on the test set
  • Under H_0 , classification impossible: \hat T \sim \mathrm{Binomial}(n, \frac12)
  • With k(x, y) = \frac14 f(x) f(y) where f(x) \in \{-1, 1\} ,
    get \MMDhat(\X, \Y) = \left\lvert \hat{T}(\X, \Y) - \frac12 \right\rvert

Deep learning and deep kernels

  • k(x, y) = \tfrac14 f(x) f(y) is one form of deep kernel
  • Deep models are usually of the form f(x) = w\tp \phi_\psic(x)
    • With a learned \phi_\psic(x) : \mathcal X \to \R^{D}
  • If we fix \psic , have f \in \cH_\psic with k_\psic(x, y) = \phi_\psic(x)\tp \phi_\psic(y)
    • Same idea as NNGP approximation
  • Generalize to a deep kernel: k_\psic(x, y) = \kappa\left( \phi_\psic(x), \phi_\psic(y) \right)

Normal deep learning \subset deep kernels

  • Take k_\psic(x, y) = \tfrac14 f_\psic(x) f_\psic(y) \fragment[1]{+ 1}
  • Final function in \cH_\psic will be a f_\psic(x) \fragment[1]{+ b}
  • With logistic loss: this is Platt scaling

“Normal deep learning \subset deep kernels” – so?

  • This does not say that deep learning is (even approximately) a kernel method
  • …despite what some people might want you to think
  • We know theoretically deep learning can learn some things faster than any kernel method [see Malach+ ICML-21 + refs]
  • But deep kernel learning ≠ traditional kernel models
    • exactly like how usual deep learning ≠ linear models

Optimizing power of MMD tests

  • Asymptotics of \MMDhat^2 give us immediately that \Pr_{H_1}\left( n \MMDhat^2 > c_\alpha \right) \approx \Phi\left( \frac{\sqrt n \MMD^2}{\sigma_{H_1}} - \frac{c_\alpha}{\sqrt n \sigma_{H_1}} \right) \MMD , \sigma_{H_1} , c_\alpha are constants: first term usually dominates
  • Pick k to maximize an estimate of \MMD^2 / \sigma_{H_1}
  • Use \MMDhat from before, get \hat\sigma_{H_1} from U-statistic theory
  • Can show uniform \mathcal O_P(n^{-\frac13}) convergence of estimator
  • Get better tests (even after data splitting)

Application: (S)MMD GANs

  • An implicit generative model:
    • A generator net outputs samples from \Qtheta
    • Minimize estimate of \MMD{\psic}(\PP^m, \Qtheta^n) on a minibatch
  • MMD GAN: \min_{\vtheta} \left[ \max_{\psic} \MMD_{\psic}(\PP, \Qtheta) \right]
  • SMMD GAN: \min_{\vtheta} \left[ \max_{\psic} \textcolor{red}{\mathrm S}\!\MMD_{\psic}(\PP, \Qtheta) \right]
    • Scaled MMD uses kernel properties to ensure smooth loss for \vtheta
      by making witness function smooth [Arbel+ NeurIPS-18]
    • Uses \hinner{f}{\partial_{x_1} k(x, \cdot)} = \partial_{x_1} f(x)
    • Standard WGAN-GP better thought of in kernel framework

Application: fair representation learning (MMD-B-FAIR) [Deka/Sutherland AISTATS-23]

  • Want to find a representation where
    • We can tell whether an applicant is “creditworthy”
    • We can't distinguish applicants by race
  • Find a good classifier with near-zero test power for race
  • Minimizing the test power criterion turns out to be hard
    • Workaround: minimize test power of a (theoretical) block test

Application: distribution regression/classification/…

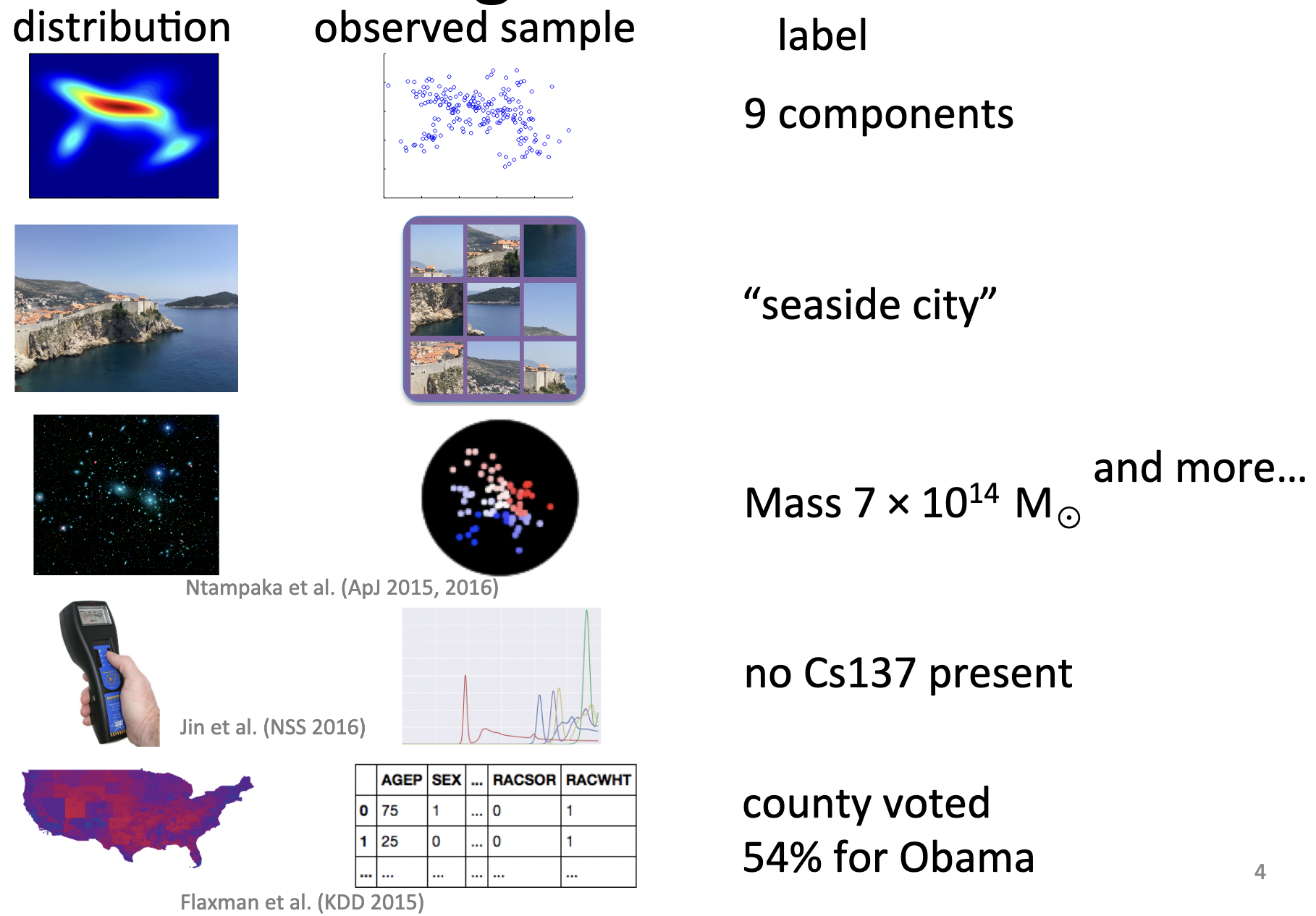
Example: age from face images [Law+ AISTATS-18]

Bayesian distribution regression: incorporate \muP uncertainty

\Biggl\{ , , , , \Biggr\} \to 35

IMDb database [Rothe+ 2015]: 400k images of 20k celebrities

Independence

  • \X \indep \Y iff \Cov(f(\X), g(\Y)) = 0 for all square-integrable f , g
  • Let's implement for RKHS functions f \in \Hx , g \in \Hy : \begin{align*} \E[\fc(\X)] \E[\gc(\Y)] &\fragment[1]{{}= \hinner[\Hx]{\fc}{\muP} \hinner[\Hy]{\muQ}{\gc}} \\&\fragment[2]{{}= \hinner[\Hx]{\fc}{(\muP \otimes \muQ) \gc}} \\ \fragment[3]{\E[\fc(\X) \gc(\Y)]} &\fragment[4]{{}= \E[ \hinner[\Hx]{\fc}{\kx(\X, \cdot)} \hinner[\Hy]{\ky(\Y, \cdot)}{\gc}]} \\&\fragment[5]{{}= \hinner[\Hx]{\fc}{ \E\left[ \kx(\X, \cdot) \otimes \ky(\Y, \cdot) \right] \, \gc }} \\ \fragment[6]{\Cov(\fc(\X), \gc(\Y))} &\fragment[6]{{}= \hinner[\Hx]{\fc}{ C_{\X\Y} \gc }} \end{align*} where C_{\X\Y} : \Hy \to \Hx is \E\left[ \kx(\X, \cdot) \otimes \ky(\Y, \cdot) \right] - \E\left[ \kx(\X, \cdot) \right] \otimes \E\left[ \ky(\Y, \cdot) \right]

Cross-covariance operator and independence

  • \Cov(\fc(\X), \gc(\Y)) = \hinner[\Hx]{\fc}{C_{\X\Y} \gc}
  • C_{\X\Y} = \E\left[ \kx(\X, \cdot) \otimes \ky(\Y, \cdot) \right] - \muP \otimes \muQ
  • If \X \indep \Y , then C_{\X\Y} = 0
  • If C_{\X\Y} = 0 , \Cov(\fc(\X), \gc(\Y)) = 0 \quad \forall \fc \in \Hx, \gc \in \Hy
  • If \kx , \ky are characteristic:
    • C_{\X\Y} = 0 implies X \indep Y [Szabó/Sriperumbudur JMLR-18]
    • \X \indep \Y iff C_{\X\Y} = 0
    • \X \indep Y iff 0 = \norm{C_{\X\Y}}_\HS^2 (sum squared singular values)
      • HSIC: "Hilbert-Schmidt Independence Criterion"

HSIC

\begin{align*} C_{\X\Y} &= \E\left[ \kx(\X, \cdot) \otimes \ky(\Y, \cdot) \right] - \muP \otimes \muQ \\ \norm{C_{\X\Y}}_{\HS}^2 &= \hNorm[\Hx \otimes \Hy]{\mu_{\mathbb{P}_{\X\Y}} - \muP \otimes \muQ}^2 \\&\fragment[1]{{}= \MMD(\mathbb{P}_{\X\Y}, \PP \times \QQ)^2} \\&\fragment[2]{{} = \E[ \kx(\X, \Xp) \ky(\Y, \Yp) ] }\\&\fragment[2]{{}\quad - 2 \E[\kx(\X, \Xp) \kx(\Y, \Ypp)] }\\&\fragment[2]{{}\quad + \E[\kx(\X, \Xp)] \E[\ky(\Y, \Yp)] } \\&\fragment[5]{{}= \E_{\substack{f \sim \mathcal{GP}(0, \kx)\\g \sim \mathcal{GP}(0, \ky)}}\left[ \Cov(f(\X), g(\Y))^2 \right] } \end{align*}
  • Linear case: C_{\X\Y} is cross-covariance matrix, HSIC is squared Frobenius norm
  • Default estimator (biased, but simple): \inner{H K_\X H}{K_\Y}_F , H = I - \mathbf{1} \mathbf{1}\tp

HSIC applications

Example: SSL-HSIC [Li+ NeurIPS-21]

  • Maximizes dependence between image features f and its identity on a minibatch
  • Using a learned deep kernel based on g

Recap

  • Point embedding k(X, \cdot) : if f \in \cH then \hinner{f}{\muP} = \E_{\X \sim \PP} f(\X)
  • Mean embedding \muP = \E k(\X, \cdot) : if f \in \cH then \hinner{f}{\muP} = \E_{\X \sim \PP} f(\X)

  • \MMD(\PP, \QQ) = \hnorm{\muP - \muQ} is 0 iff \PP = \QQ (for characteristic kernels)
  • \HSIC(\X, \Y) = \hnorm[\HS]{C_{\X\Y}} = \MMD(\mathbb{P}_{\X\Y}, \PP \times \QQ)^2 is 0 iff \X \indep \Y
    (for characteristic \kx , \ky ...or slightly weaker)

  • Often need to learn a kernel for good performance on complicated data
    • Can often do end-to-end for downstream loss, asymptotic test power, …

More resources