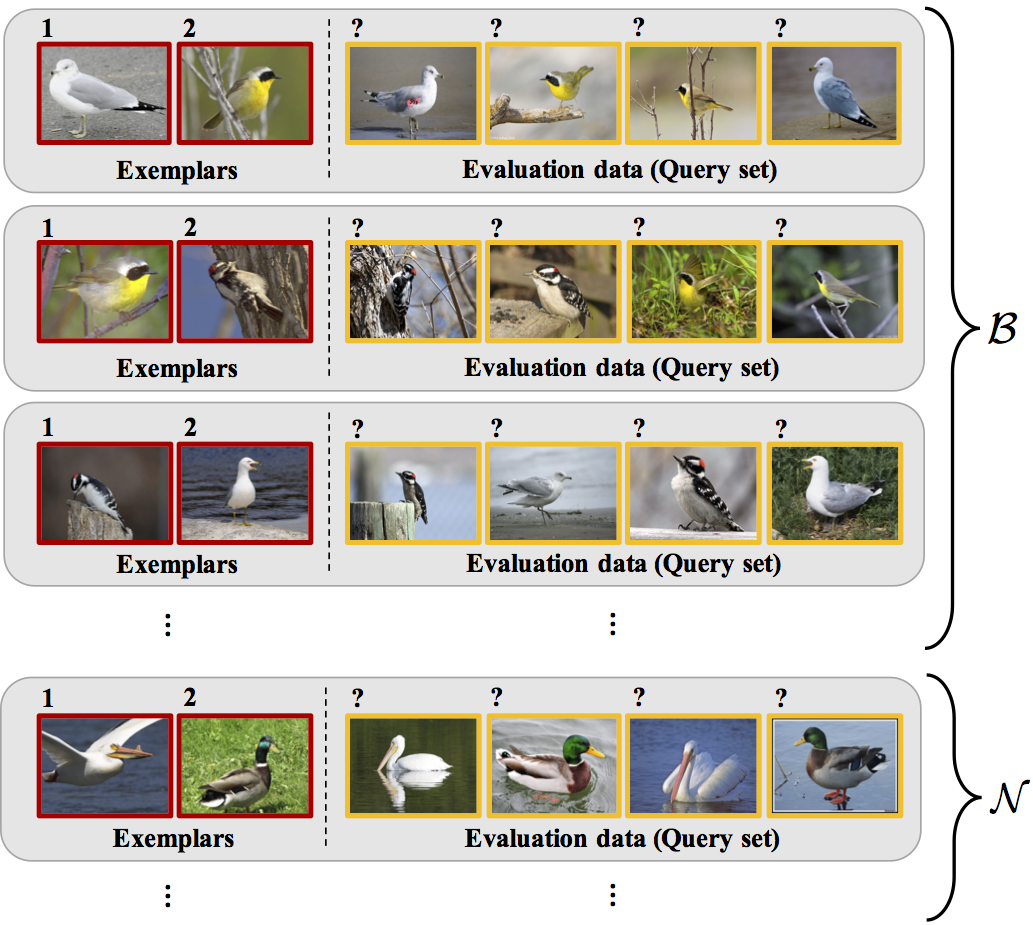
Are these datasets the same?
Learning kernels for efficient and fair two-sample tests
Danica J. Sutherland(she/her)
University of British Columbia (UBC) / Alberta Machine Intelligence Institute (Amii)
new!
Namrata Deka
TrustML - 15 Feb 2022
(Swipe or arrow keys to move through slides; for a menu to jump; to show more.)
Data drift
- The textbook ML setting:
- Train on i.i.d. samples from some distribution,
- Training error test error on
- So our model should be good on more samples from
- Really:
- Train on “i.i.d. samples from some distribution, ”
- Training error might vaguely correlate with test error on
- Deploy it on some distribution , might be sort of like
- and probably changes over time…
This talk
Based on samples and :
- How is different from ?
- Is close enough to for our model?
- Is ?
Two-sample testing
- Given samples from two unknown distributions
- Question: is ?
- Hypothesis testing approach:
- Reject if test statistic
- Do smokers/non-smokers get different cancers?
- Do Brits have the same friend network types as Americans?
- When does my laser agree with the one on Mars?
- Are storms in the 2000s different from storms in the 1800s?
- Does presence of this protein affect DNA binding? [MMDiff2]
- Do these dob and birthday columns mean the same thing?
- Does my generative model match ?
- Independence testing: is ?
What's a hypothesis test again?
Permutation testing to find
Need
: th quantile of
Need a to estimate the difference between distributions, based on samples
Our choice of : the Maximum Mean Discrepancy (MMD)
This is a kernel-based distance between distributions
What's a kernel again?
- Linear classifiers: ,
- Use a “richer” :
- Can avoid explicit ; instead
- “Kernelized” algorithms access data only through
- gives kernel notion of smoothness
Reproducing Kernel Hilbert Space (RKHS)
- Ex: Gaussian RBF / exponentiated quadratic / squared exponential / …
- Some functions with small :
Maximum Mean Discrepancy (MMD)
The sup is achieved by
Estimating MMD
 |  |  | |
|---|---|---|---|
 | 1.0 | 0.2 | 0.6 |
 | 0.2 | 1.0 | 0.5 |
 | 0.6 | 0.5 | 1.0 |
 |  |  | |
|---|---|---|---|
 | 1.0 | 0.8 | 0.7 |
 | 0.8 | 1.0 | 0.6 |
 | 0.7 | 0.6 | 1.0 |
 |  |  | |
|---|---|---|---|
 | 0.3 | 0.1 | 0.2 |
 | 0.2 | 0.3 | 0.3 |
 | 0.2 | 0.1 | 0.4 |
MMD as feature matching
- is the feature map for
- If , , then
the MMD is distance between means - Many kernels: infinite-dimensional
MMD-based tests
- If is characteristic, iff
- Efficient permutation testing for
- : converges in distribution
- : asymptotically normal
- Any characteristic kernel gives consistent test…eventually
- Need enormous if kernel is bad for problem
Classifier two-sample tests
- is the accuracy of on the test set
- Under , classification impossible:
- With where ,
get
Deep learning and deep kernels
- is one form of deep kernel
- Deep models are usually of the form
- With a learned
- If we fix , have with
- Same idea as NNGP approximation
- Generalize to a deep kernel:
Normal deep learning deep kernels
- Take
- Final function in will be
- With logistic loss: this is Platt scaling

So what?
- This definitely does not say that deep learning is (even approximately) a kernel method
- …despite what some people might want you to think
![]()
- We know theoretically deep learning can learn some things faster than any kernel method [see Malach+ ICML-21 + refs]
- But deep kernel learning ≠ traditional kernel models
- exactly like how usual deep learning ≠ linear models
Optimizing power of MMD tests
- Asymptotics of give us immediately that , , are constants: first term usually dominates
- Pick to maximize an estimate of
- Use from before, get from U-statistic theory
- Can show uniform convergence of estimator
Blobs dataset
Blobs kernels
Blobs results
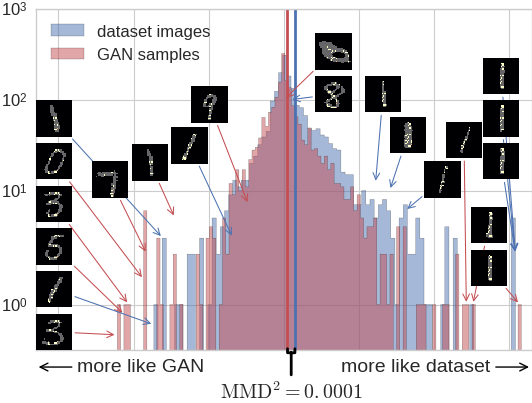
Investigating a GAN on MNIST
CIFAR-10 vs CIFAR-10.1


| ME | SCF | C2ST | MMD-O | MMD-D |
|---|---|---|---|---|
| 0.588 | 0.171 | 0.452 | 0.316 | 0.744 |
Ablation vs classifier-based tests
| Cross-entropy | Max power | |||||
|---|---|---|---|---|---|---|
| Dataset | Sign | Lin | Ours | Sign | Lin | Ours |
| Blobs | 0.84 | 0.94 | 0.90 | – | 0.95 | 0.99 |
| High- Gauss. mix. | 0.47 | 0.59 | 0.29 | – | 0.64 | 0.66 |
| Higgs | 0.26 | 0.40 | 0.35 | – | 0.30 | 0.40 |
| MNIST vs GAN | 0.65 | 0.71 | 0.80 | – | 0.94 | 1.00 |
But…
- What if you don't have much data for your testing problem?
- Need enough data to pick a good kernel
- Also need enough test data to actually detect the difference
- Best split depends on best kernel's quality / how hard to find
- Don't know that ahead of time; can't try more than one
Meta-testing
- One idea: what if we have related problems?
- Similar setup to meta-learning:
![]() (from Wei+ 2018)
(from Wei+ 2018)
Meta-testing for CIFAR-10 vs CIFAR-10.1
- CIFAR-10 has 60,000 images, but CIFAR-10.1 only has 2,031
- Where do we get related data from?
- One option: set up tasks to distinguish classes of CIFAR-10 (airplane vs automobile, airplane vs bird, ...)
One approach (MAML-like)
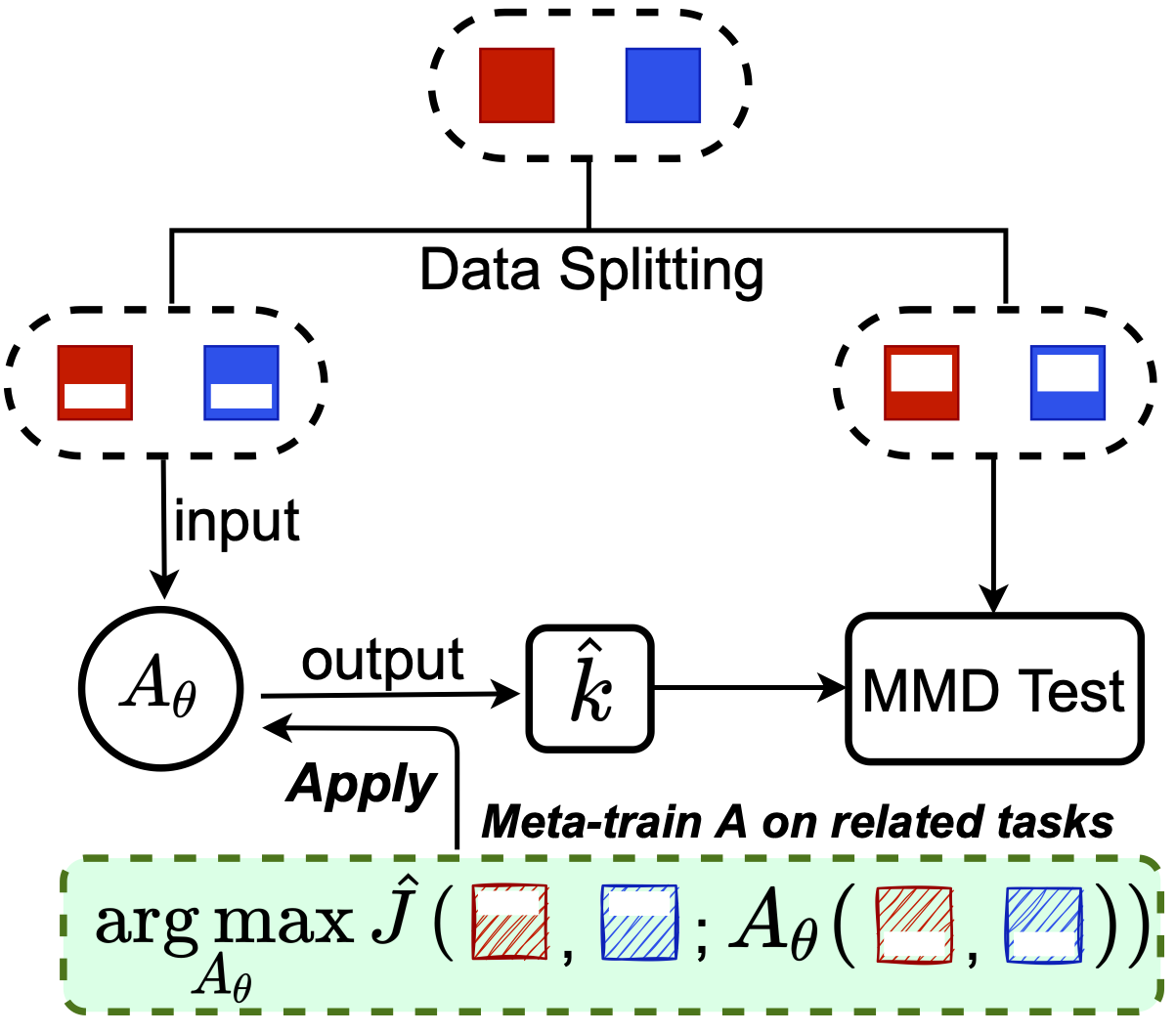
is, e.g., 5 steps of gradient descent
we learn the initialization, maybe step size, etc
we learn the initialization, maybe step size, etc

This works, but not as well as we'd hoped…
Initialization might work okay on everything, not really adapt
Another approach: Meta-MKL
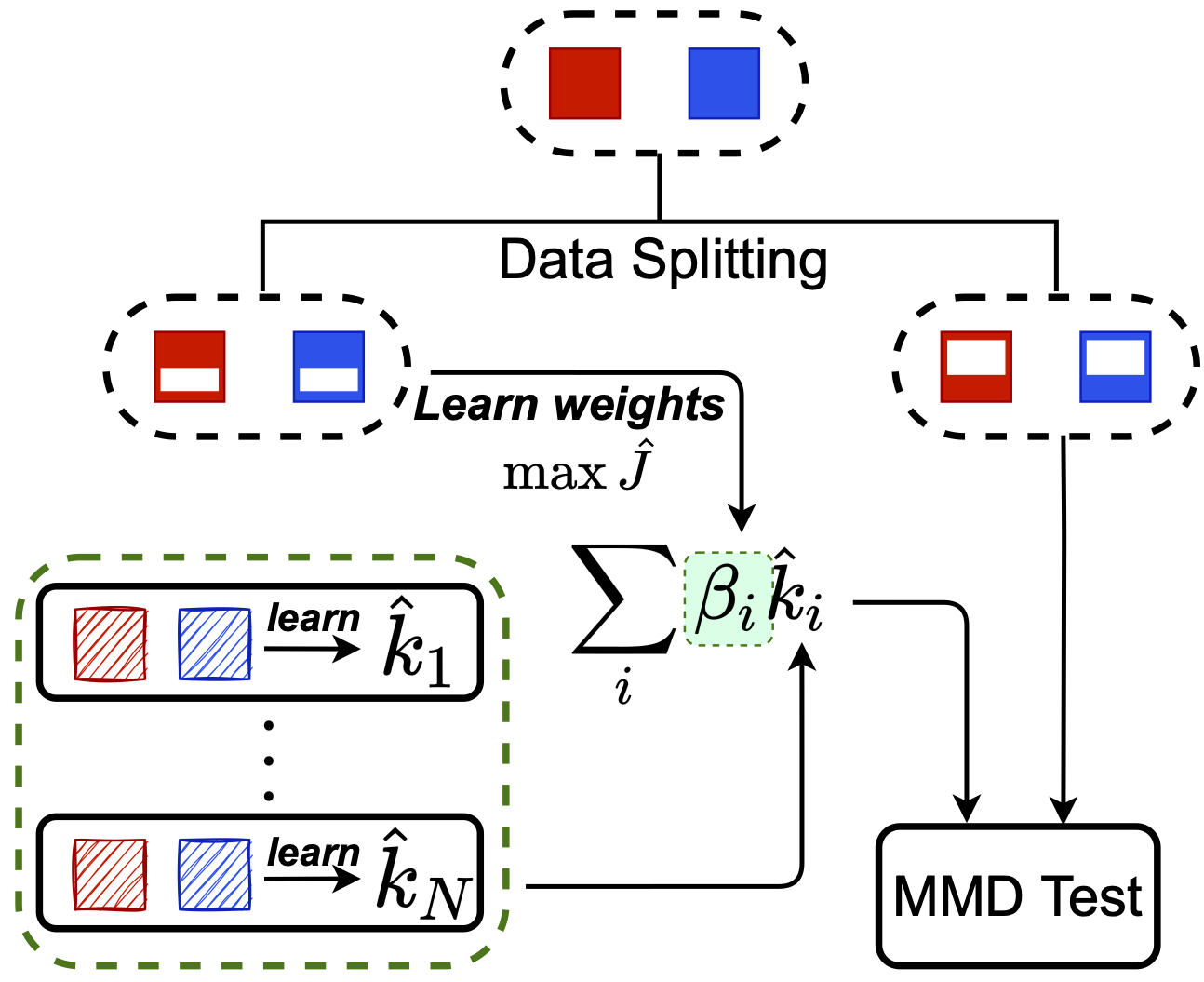
Inspired by classic multiple kernel learning
Only need to learn linear combination on test task:
much easier
Only need to learn linear combination on test task:
much easier

Theoretical analysis for Meta-MKL
- Same big-O dependence on test task size 😐
- But multiplier is much better:
based on number of meta-training tasks, not on network size - Coarse analysis: assumes one meta-tasks is “related” enough
- We compete with picking the single best related kernel
- Haven't analyzed meaningfully combining related kernels (yet!)
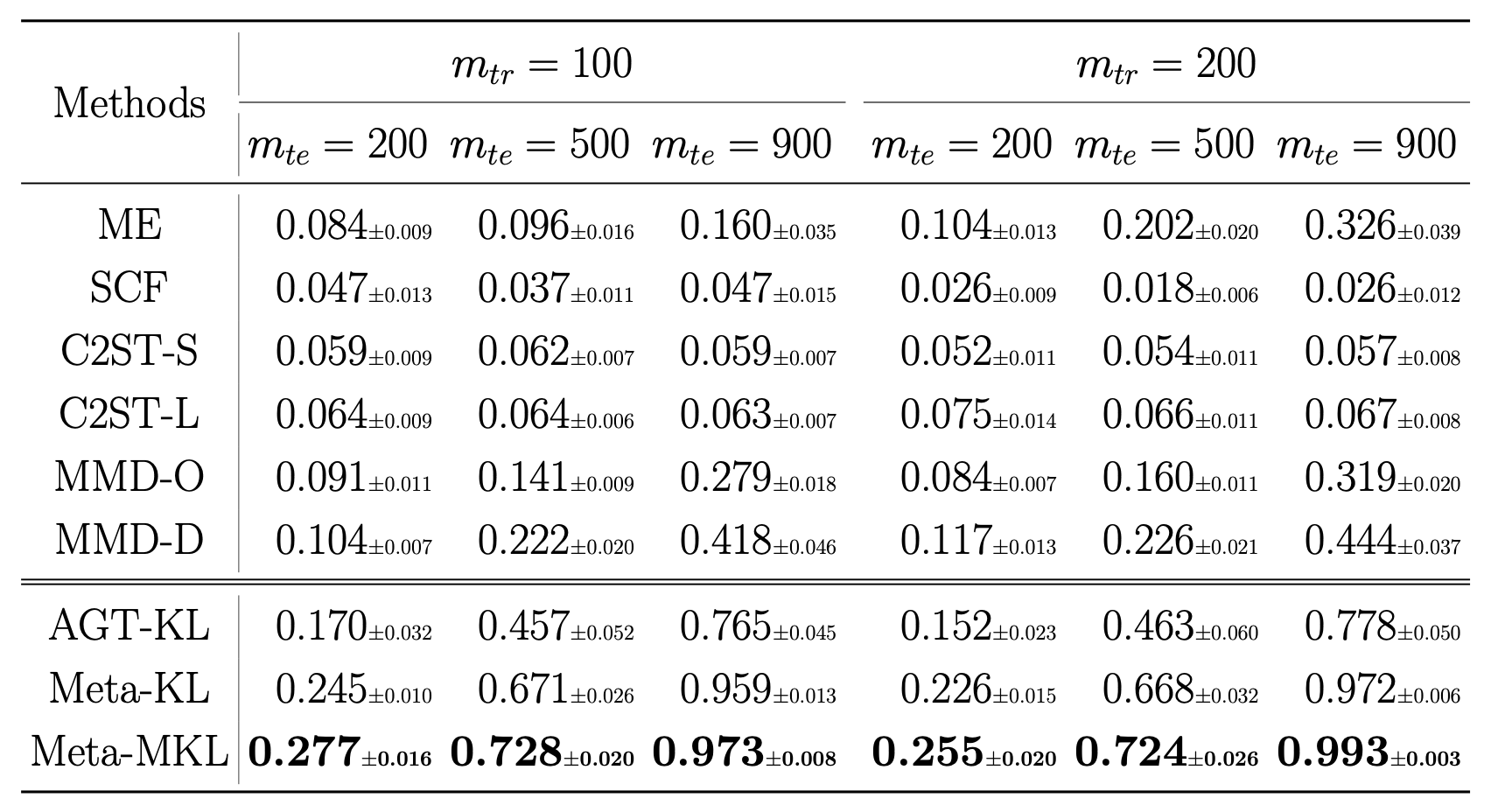
Results on CIFAR-10.1
But...
- Sometimes we know ahead of time that there are differences that we don't care about
- In the MNIST GAN criticism, initial attempt just picked out that the GAN outputs numbers that aren't one of the 256 values MNIST has
- Can we find a kernel that can distinguish from ,
but can't distinguish from ? - Also useful for fair representation learning
- e.g. can distinguish “creditworthy” vs not,
can't distinguish by race
- e.g. can distinguish “creditworthy” vs not,
High on one power, low on another
Choose with
- First idea:
- No good: doesn't balance power appropriately
- Second idea:
- Can estimate inside the optimization
- Better, but tends to “stall out” in minimizing
Block estimator [Zaremba+ NeurIPS-13]
- Use previous on blocks, each of size
- Final estimator: average of each block's estimate
- Each block has previous asymptotics
- Central limit theorem across blocks
- Power is
MMD-B-Fair
- Choose as
- is the power of a test with blocks of size
- We don't actually use a block estimator computationally
- , have nothing to do with minibatch size
- Representation learning:
- Deep kernel is
- could be deep itself, with adversarial optimization
- For now, just Gaussians with different lengthscales
Adult
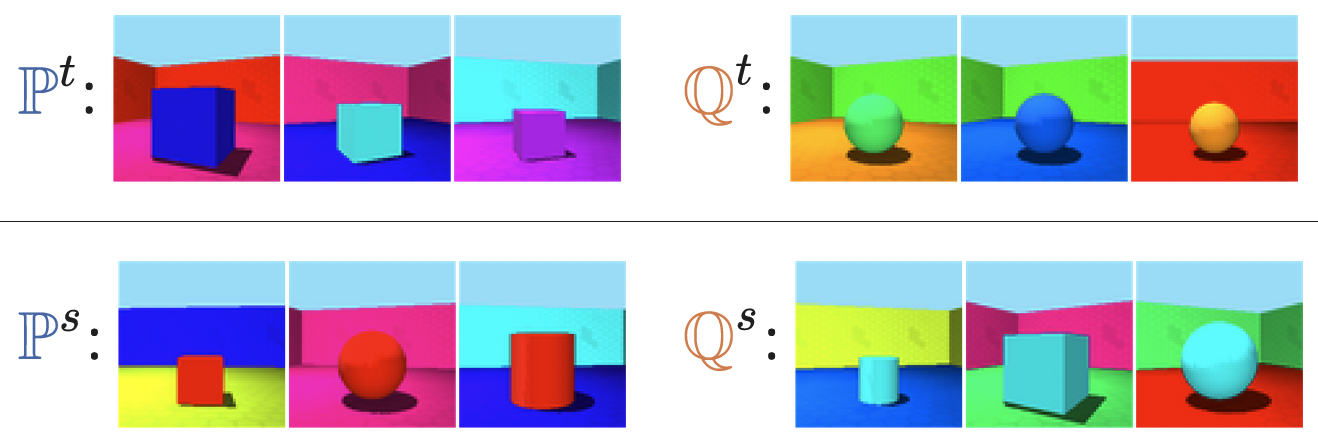
Shapes3D
:  | :  |
:  | :  |
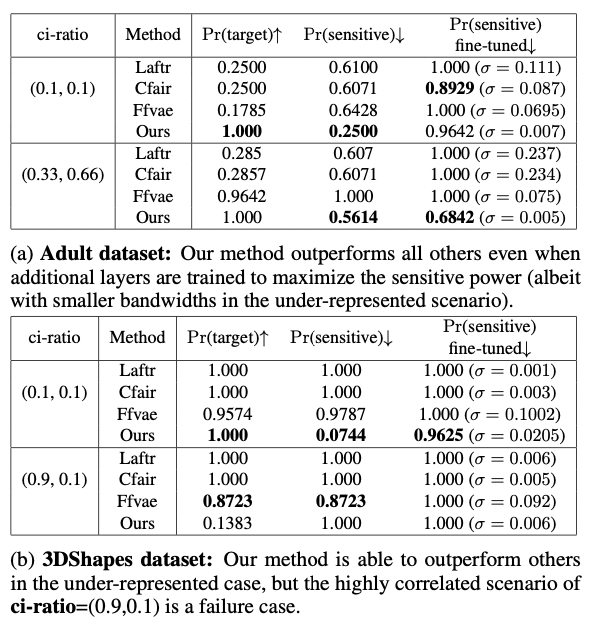
Multiple targets / sensitive attributes
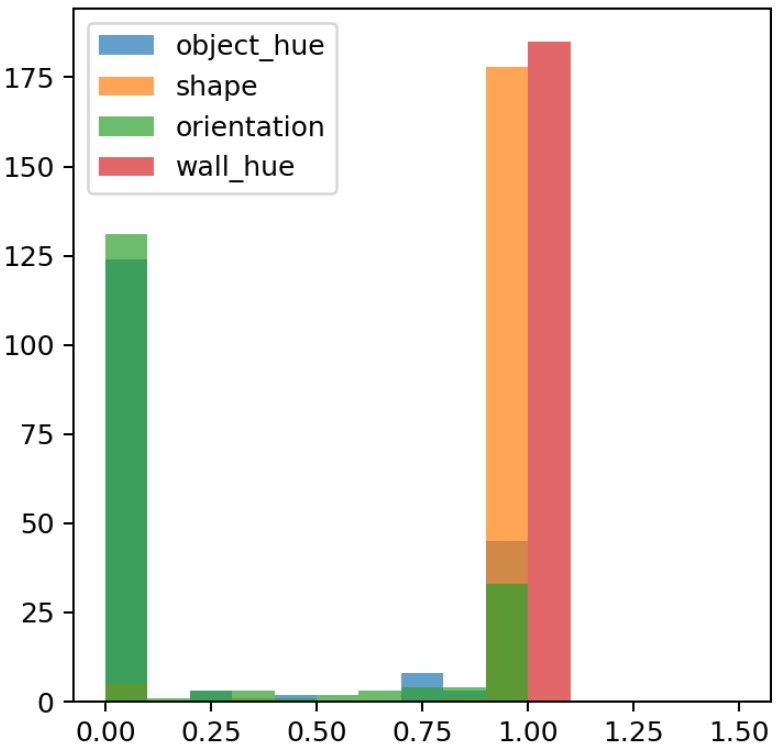 power on minibatches
power on minibatchesRemaining challenges
- MMD-B-Fair:
- When and are very correlated
- For attributes with many values (use HSIC?)
- Meta-testing: more powerful approaches, better analysis
- When , can we tell how they're different?
- Methods so far: low-, and/or points w/ large critic value
![]()
![]()
![]()
![]()
![]()
- Methods so far: low-, and/or points w/ large critic value
- Avoid the need for data splitting (selective inference)
- Kübler+ NeurIPS-20 gave one method, but very limited
A good takeaway
Combining a deep architecture with a kernel machine that takes the higher-level learned representation as input can be quite powerful.
— Y. Bengio & Y. LeCun (2007), “Scaling Learning Algorithms towards AI”