\definecolor{cb1}{RGB}{76,114,176} \definecolor{cb2}{RGB}{221,132,82} \definecolor{cb3}{RGB}{85,168,104} \definecolor{cb4}{RGB}{196,78,82} \definecolor{cb5}{RGB}{129,114,179} \definecolor{cb6}{RGB}{147,120,96} \definecolor{cb7}{RGB}{218,139,195} \DeclareMathOperator{\argmin}{argmin} \DeclareMathOperator{\argmax}{argmax} \DeclareMathOperator{\D}{\mathcal{D}} \DeclareMathOperator*{\E}{\mathbb{E}} \DeclareMathOperator*{\Var}{Var} \DeclareMathOperator{\mean}{mean} \DeclareMathOperator{\W}{\mathcal{W}} \DeclareMathOperator{\KL}{KL} \DeclareMathOperator{\JS}{JS} \DeclareMathOperator{\mmd}{MMD} \DeclareMathOperator{\smmd}{SMMD} \DeclareMathOperator{\mmdhat}{\widehat{MMD}} \newcommand{\optmmd}[1][\Psic]{\operatorname{\mathcal{D}_\mathrm{MMD}^{#1}}} \DeclareMathOperator{\optmmdhat}{\hat{\mathcal{D}}_\mathrm{MMD}} \newcommand{\optsmmdp}{\operatorname{\mathcal{D}_\mathrm{SMMD}}} \newcommand{\optsmmd}[1][\Psic]{\operatorname{\mathcal{D}_\mathrm{SMMD}^{\SS,#1,\lambda}}} \newcommand{\ktop}{k_\mathrm{top}} \newcommand{\lip}{\mathrm{Lip}} \newcommand{\tp}{^\mathsf{T}} \newcommand{\F}{\mathcal{F}} \newcommand{\h}{\mathcal{H}} \newcommand{\hk}{{\mathcal{H}_k}} \newcommand{\Xc}{\mathcal{X}} \newcommand{\cP}[1]{{\color{cb1} #1}} \newcommand{\PP}{\cP{\mathbb P}} \newcommand{\pp}{\cP{p}} \newcommand{\X}{\cP{X}} \newcommand{\Xp}{\cP{X'}} \newcommand{\Pdata}{\cP{\mathbb{P}_\mathrm{data}}} \newcommand{\cQ}[1]{{\color{cb2} #1}} \newcommand{\QQ}{\cQ{\mathbb Q}} \newcommand{\qtheta}{\cQ{q_\theta}} \newcommand{\Y}{\cQ{Y}} \newcommand{\Yp}{\cQ{Y'}} \newcommand{\thetac}{\cQ{\theta}} \newcommand{\vtheta}{\thetac} \newcommand{\Qtheta}{\QQ_\thetac} \newcommand{\Gtheta}{\cQ{G_\theta}} \newcommand{\cZ}[1]{{\color{cb5} #1}} \newcommand{\Z}{\cZ{Z}} \newcommand{\Zc}{\cZ{\mathcal Z}} \newcommand{\ZZ}{\cZ{\mathbb Z}} \newcommand{\cpsi}[1]{{\color{cb3} #1}} \newcommand{\psic}{\cpsi{\psi}} \newcommand{\Psic}{\cpsi{\Psi}} \newcommand{\Dpsi}{\cpsi{D_\psi}} \newcommand{\SS}{\cpsi{\mathbb{S}}} \newcommand{\Xtilde}{\cpsi{\tilde{X}}} \newcommand{\Xtildep}{\cpsi{\tilde{X}'}} \newcommand{\R}{\mathbb R} \newcommand{\ud}{\mathrm d}

Better GANs by Using Kernels

D.J. Sutherland
TTIC
Michael Arbel
UCL
Mikołaj Bińkowski
Imperial
Arthur Gretton
UCL
\D\left( \rule{0cm}{1.1cm} \right. , \; \left. \rule{0cm}{1.1cm} \right)

UMass Amherst, Sep 30 2019

(Swipe or arrow keys to move through slides; m for a menu to jump; ? for help. Vertical slides are backups that I probably won't show in the talk.)

Implicit generative models

Given samples from a distribution \PP over \Xc ,
we want a model that can produce new samples from \Qtheta \approx \PP


\X \sim \PP

\Y \sim \Qtheta

Why implicit generative models?

How to generate images things?

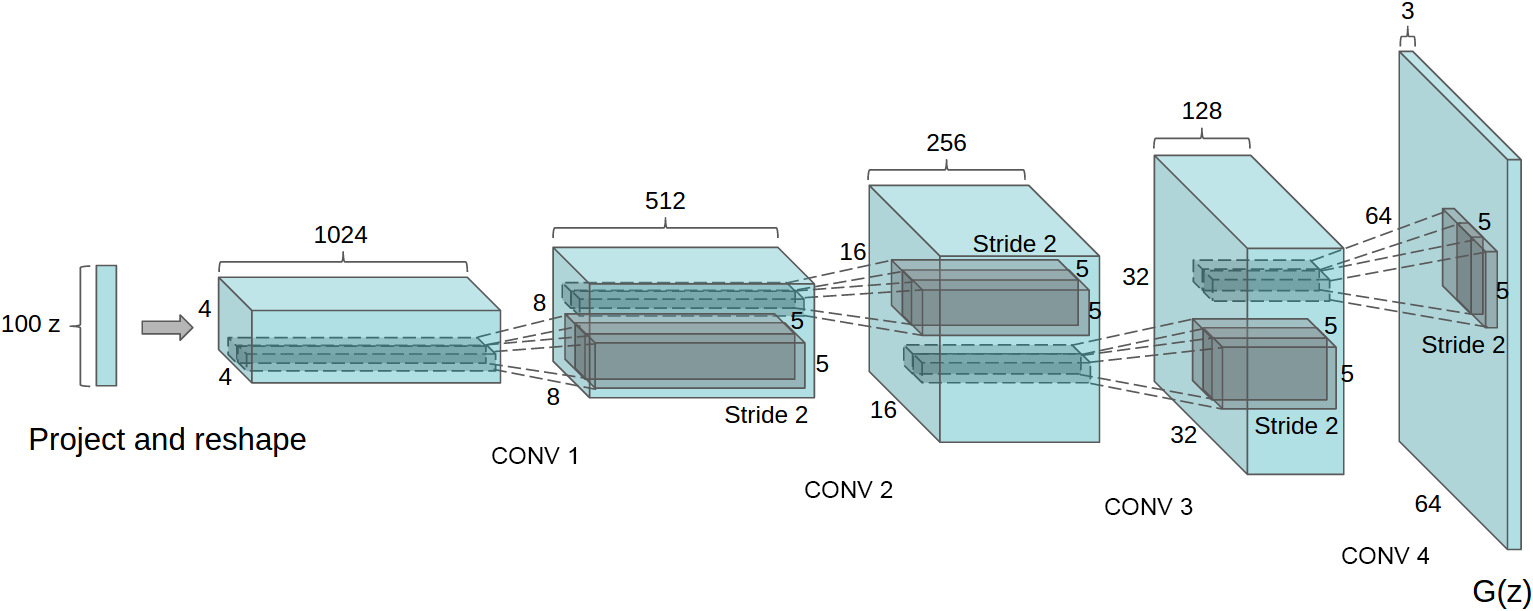
One choice: with a generator!

Fixed distribution of latents: \Z \sim \mathrm{Uniform}\left( [-1, 1]^{100} \right)

Maps through a network: G_\thetac(\Z) \sim \Qtheta

How to choose \thetac ?

GANs: trick a discriminator [Goodfellow+ NeurIPS-14]

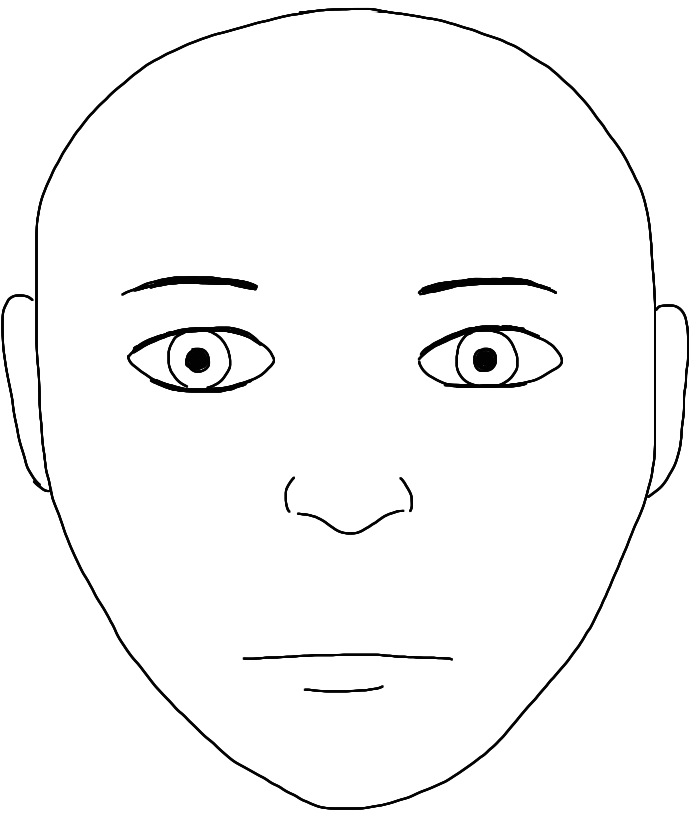
Generator ( \Qtheta )

Discriminator

Target ( \PP )

Is this real?

No way! \Pr(\text{real}) = 0.03

:( I'll try harder…

⋮

Is this real?

Umm… \Pr(\text{real}) = 0.48

One view: distances between distributions

  • What happens when \Dpsi is at its optimum?
  • If distributions have densities, \Dpsi^*(x) = \frac{\pp(x)}{\pp(x) + \qtheta(x)}
  • If \Dpsi stays optimal throughout, \vtheta tries to minimize \!\!\!\! \frac12 \E_{\X \sim \PP}\left[ \log \frac{\pp(\X)}{\pp(\X) + \qtheta(\X)} \right] + \frac12 \E_{\Y \sim \Qtheta}\left[ \log \frac{\qtheta(\X)}{\pp(\X) + \qtheta(\X)} \right] which is \JS(\PP, \Qtheta) - \log 2

JS with disjoint support [Arjovsky/Bottou ICLR-17]

\begin{align} \JS(\PP, \Qtheta) &= \frac12 \int \pp(x) \log \frac{\pp(x)}{\frac12 \pp(x) + \frac12 \qtheta(x)} \ud x \\&+ \frac12 \int \qtheta(x) \log \frac{\qtheta(x)}{\frac12 \pp(x) + \frac12 \qtheta(x)} \ud x \end{align}

  • If \PP and \Qtheta have (almost) disjoint support \frac12 \int \pp(x) \log \frac{\pp(x)}{\frac12 \pp(x)} \ud x \fragment{= \frac12 \int \pp(x) \log(2) \ud x} \fragment{= \frac12 \log 2} so \JS(\PP, \Qtheta) = \log 2

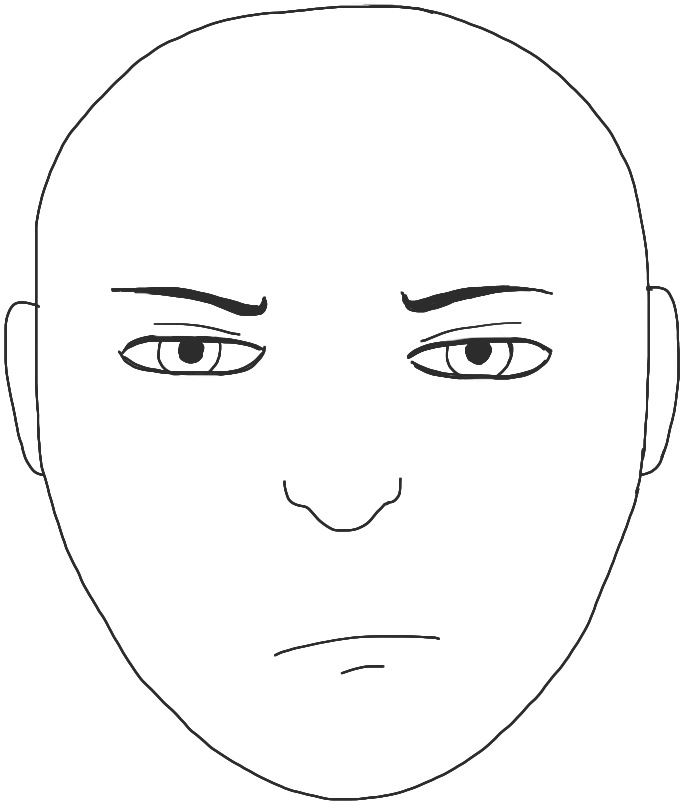
Discriminator point of view

Generator ( \Qtheta )

Discriminator

Target ( \PP )

Is this real?

No way! \Pr(\text{real}) = 0.00

:( I don't know how to do any better…

How likely is disjoint support?

  • At initialization, pretty reasonable:
    \PP :
    \Qtheta :
  • Remember we might have \Gtheta : \R^{100} \to \R^{64 \times 64 \times 3}
  • For usual \Gtheta , \Qtheta is supported on a countable union of
    manifolds with dim \le 100
  • “Natural image manifold” usually considered low-dim
  • No chance that they'd align at init, so \JS(\PP, \Qtheta) = \log 2

Path to a solution: integral probability metrics

\D_\F(\PP, \QQ) = \sup_{f \in \F} \E_{\X \sim \PP}[f(\X)] - \E_{\Y \sim \QQ}[f(\Y)]

f : \Xc \to \R is a critic function

Total variation: \color{cb4}{\F} = \{ f : f \text{ continuous, } \lvert f(x) \rvert \le 1 \}

Wasserstein: \color{cb5}{\F} = \{ f : \lVert f \rVert_\lip \le 1 \}

Maximum Mean Discrepancy [Gretton+ 2012]

\mmd_k(\PP, \QQ) = \sup_{f : \lVert f \rVert_\hk \le 1} \E_{\X \sim \PP}[f(\X)] - \E_{\Y \sim \QQ}[f(\Y)]

Kernel k : \Xc \times \Xc \to \R – a “similarity” function

f^*(t) \propto \E_{\X \sim \PP} k(t, \X) - \E_{\Y \sim \QQ} k(t, \Y)

For many kernels, \mmd(\PP, \QQ) = 0 iff \PP = \QQ

MMD as feature matching

\mmd_k(\PP, \QQ) = \left\lVert \E_{\X \sim \PP}[ \varphi(\X) ] - \E_{\Y \sim \QQ}[ \varphi(\Y) ] \right\rVert_{\hk}

  • \varphi : \Xc \to \hk is the feature map for k(x, y) = \langle \varphi(x), \varphi(y) \rangle
  • If k(x, y) = x\tp y , \varphi(x) = x ; MMD is distance between means
  • Many kernels: infinite-dimensional \hk

Derivation of MMD

Reproducing property: if f \in \hk , f(x) = \langle f, \varphi(x) \rangle_\hk

\begin{align} \mmd&_k(\PP, \QQ) = \sup_{\lVert f \rVert_\hk \le 1} \E_{\X \sim \PP}[f(\X)] - \E_{\Y \sim \QQ}[f(\Y)] \\&\fragment[1]{ = \sup_{\lVert f \rVert_\hk \le 1} \E_{\X \sim \PP}[\langle f, \varphi(\X) \rangle_\hk] - \E_{\Y \sim \QQ}[\langle f, \varphi(\Y) \rangle_\hk] } \\&\fragment[2]{ = \sup_{\lVert f \rVert_\hk \le 1} \left\langle f, \E_{\X \sim \PP}[\varphi(\X)] - \E_{\Y \sim \QQ}[\varphi(\Y)] \right\rangle_\hk } \\&\fragment[3]{= %\left\lVert % \E_{\X \sim \PP}[\varphi(\X)] %- \E_{\Y \sim \QQ}[\varphi(\Y)] %\right\rVert_\hk \sup_{\lVert f \rVert_\hk \le 1} \left\langle f, \mu^k_\PP - \mu^k_\QQ \right\rangle_\hk } \fragment[4]{= \left\lVert \mu^k_\PP - \mu^k_\QQ \right\rVert_\hk } \\ \fragment[5]{\langle \mu_\PP^k, \,} & \fragment[5]{% \mu_\QQ^k \rangle_\hk = \E_{\substack{\X \sim \PP\\\Y \sim \QQ}} \langle \varphi(\X), \varphi(\Y) \rangle_\hk = \E_{\substack{\X \sim \PP\\\Y \sim \QQ}} k(\X, \Y) } \end{align}

Estimating MMD

\begin{gather} \mmd_k^2(\PP, \QQ) % = \E_{\substack{\X, \Xp \sim \PP\\\Y, \Yp \sim \QQ}}\left[ % k(\X, \Xp) % - 2 k(\X, \Y) % + k(\Y, \Yp) % \right] = \E_{\X, \Xp \sim \PP}[k(\X, \Xp)] + \E_{\Y, \Yp \sim \QQ}[k(\Y, \Yp)] - 2 \E_{\substack{\X \sim \PP\\\Y \sim \QQ}}[k(\X, \Y)] \\ \fragment[0]{ \mmdhat_k^2(\X, \Y) = \fragment[1][highlight-current-red]{\mean(K_{\X\X})} + \fragment[2][highlight-current-red]{\mean(K_{\Y\Y})} - 2 \fragment[3][highlight-current-red]{\mean(K_{\X\Y})} } \end{gather}

K_{\X\X}

1.00.20.6
0.21.00.5
0.60.51.0

K_{\Y\Y}

1.00.80.7
0.81.00.6
0.70.61.0

K_{\X\Y}

0.30.10.2
0.20.30.3
0.20.10.4

MMD as loss [Li+ ICML-15, Dziugaite+ UAI-15]

  • No need for a discriminator – just minimize \mmdhat_k !
  • Continuous loss, gives “partial credit”

Generator ( \Qtheta )

Critic

Target ( \PP )

How are these?

Not great! \mmdhat(\Qtheta, \PP) = 0.75

:( I'll try harder…

⋮

MMD models [Li+ ICML-15, Dziugaite+ UAI-15]

MNIST, mix of Gaussian kernels


\Pdata

\Qtheta

Celeb-A, mix of rational quadratic + linear kernels


\Pdata

\Qtheta

Deep kernels

\begin{gather} k_\psic(x, y) = \ktop(\phi_\psic(x), \phi_\psic(y)) \\ \phi_\psic : \mathcal{X} \to \R^D \qquad k_\psic : \R^D \times \R^D \to \R \end{gather}
  • \ktop usually Gaussian, linear, …

MMD loss with a deep kernel

k(x, y) = \ktop(\phi(x), \phi(y))

  • \phi : \Xc \to \R^{2048} from pretrained Inception net
  • \ktop simple: exponentiated quadratic or polynomial

\Pdata

\Qtheta

We just got adversarial examples!


[anishathalye/obfuscated-gradients]

Optimized MMD: MMD GANs [Li+ NeurIPS-17]

  • Don't just use one kernel, use a class parameterized by \psic : k_\psic(x, y) = \ktop(\phi_\psic(x), \phi_\psic(y))
  • New distance based on all these kernels: \begin{align*} \optmmd(\PP, \QQ) &= \sup_{\psic \in \Psic} \mmd_{\psic}(\PP, \QQ) %\\&= \sup_{\substack{f : \lVert f \rVert_{\h_{k_\psic}} \le 1\\\psic \in \Psic}} % \E_{\X \sim \PP}[f(\X)] - \E_{\Y \sim \QQ}[f(\Y)] \end{align*}
  • Minimax optimization problem \inf_\thetac \sup_\psic \mmd_\psic(\Pdata, \Qtheta)

Non-smoothness of Optimized MMD

Illustrative problem in \R , DiracGAN [Mescheder+ ICML-18]:

  • Just need to stay away from tiny bandwidths \psi
  • …deep kernel analogue is hard.
  • Instead, keep witness function from being too steep
  • \sup_x \lVert \nabla f(x) \rVert would give Wasserstein
    • Nice distance, but hard to estimate
  • Control \lVert \nabla f(\Xtilde) \rVert on average, near the data

MMD GANs versus WGANs

  • Linear- \ktop MMD GAN, k(x, y) = \phi(x) \phi(y) :
    \begin{gather} \text{loss} %= \mmd_\phi(\PP, \QQ) = \lvert \E_\PP \phi(\X) - \E_\QQ \phi(\Y) \rvert \\ f(t) = \operatorname{sign}\left( \E_\PP \phi(\X) - \E_\QQ \phi(\Y) \right) \phi(t) \end{gather}
  • WGAN has:
    \begin{gather} \text{loss} = \E_\PP \phi(\X) - \E_\QQ \phi(\Y) \\ f(t) = \phi(t) \end{gather}
  • We were just trying something like an unregularized WGAN…

MMD-GAN with gradient control

  • If \Psic gives uniformly Lipschitz critics, \optmmd is smooth
  • Original MMD-GAN paper [Li+ NeurIPS-17]: box constraint
  • We [Bińkowski+ ICLR-18] used gradient penalty on critic instead
    • Better in practice, but doesn't fix the Dirac problem…

New distance: Scaled MMD

Want to ensure \E_{\Xtilde \sim \SS}[ \lVert \nabla f(\Xtilde) \rVert^2 ] \le 1

Can do directly with kernel properties…but too expensive!

Guaranteed if \lVert f \rVert_\hk \le \sigma_{\SS,k,\lambda}

\sigma_{\SS,k,\lambda} := \left( \lambda + \E_{\Xtilde \sim \SS}\left[ k(\Xtilde, \Xtilde) + [\nabla_1 \!\cdot\! \nabla_2 k](\Xtilde, \Xtilde) %+ \sum_{i=1}^d \frac{\partial^2 k(y, z)}{\partial y_i \partial z_i} \Bigg\rvert_{(y,z) = (\Xtilde, \Xtilde)} \right] \right)^{-\frac12}

Gives distance \smmd_{\SS,k,\lambda}(\PP, \QQ) = \sigma_{\SS,k,\lambda} \mmd_k(\PP, \QQ)

\begin{align} \optmmd \text{ has } & \F = \bigcup_{\psic \in \Psic} \left\{ f : \lVert f \rVert_{\h_{\psic}} \le 1 \right\} \\ \optsmmd \text{ has } & \F = \bigcup_{\psic \in \Psic} \left\{ f : \lVert f \rVert_{\h_{\psic}} \le \sigma_{\SS,k,\lambda} \right\} \end{align}

Deriving the Scaled MMD

\begin{gather} \fragment[0]{\E_{\Xtilde \sim \SS}[ f(\Xtilde)^2 ] + } \E_{\Xtilde \sim \SS}[ \lVert \nabla f(\Xtilde) \rVert^2 ] \fragment[0]{+ \lambda \lVert f \rVert_\h^2} \le 1 \\ \fragment{ \E_{\Xtilde \sim \SS}[ f(\Xtilde)^2 ] = \left\langle f, \E_{\Xtilde \sim \SS}\left[ \varphi(\Xtilde) \otimes \varphi(\Xtilde) \right] f \right\rangle_\h } \\ \fragment{ \E_{\Xtilde \sim \SS}[ \lVert \nabla f(\Xtilde) \rVert^2 ] = \left\langle f, \E_{\Xtilde \sim \SS}\left[ \sum_{i=1}^d \partial_i \varphi(\Xtilde) \otimes \partial_i \varphi(\Xtilde) \right] f \right\rangle_\h } \end{gather}

Constraint can be written \langle f, D_\lambda f \rangle_\h \le 1

\langle f, D_\lambda f \rangle_\h \fragment{\le \lVert D_\lambda \rVert \, \lVert f \rVert_\h^2} \fragment{ \le \sigma_{\SS,k,\lambda}^{-2} \lVert f \rVert_\h^2}

Smoothness of \D_\mathrm{SMMD}

Theorem: \optsmmd is continuous.

If \SS has a density; \ktop is Gaussian/linear/…; \phi_\psic is fully-connected, Leaky-ReLU, non-increasing width; all weights in \Psic have bounded condition number; then

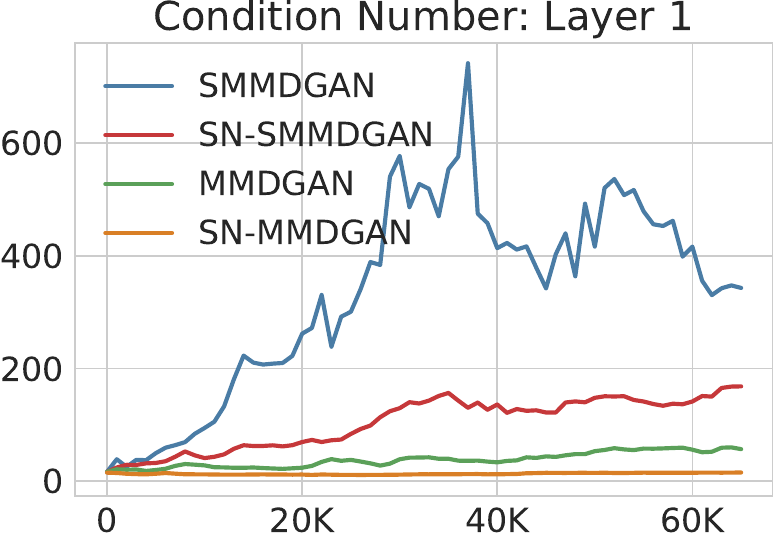
\W(\QQ_n, \PP) \to 0 \text{ implies } \optsmmd(\QQ_n, \PP) \to 0 .

Keeping weight condition numbers bounded

  • Spectral parameterization [Miyato+ ICLR-18]:
  • W = \gamma \bar W / \lVert \bar W \rVert_\mathrm{op} ; learn \gamma and \bar W freely
  • Encourages diversity without limiting representation

Rank collapse

  • Occasional optimization failure without spectral param:
    • Generator doing reasonably well
    • Critic filters become low-rank
    • Generator corrects it by breaking everything else
    • Generator gets stuck

What if we just did spectral normalization?

  • W = \bar W / \lVert \bar W \rVert_\text{op} , so that \lVert W \rVert_\text{op} = 1 , \lVert \phi_\psic \rVert_L \le 1
  • Works well for original GANs [Miyato+ ICLR-18]
  • …but doesn't work at all as only constraint in a WGAN
  • Limits representation too much
    • In DiracGAN, only allows bandwidth 1
    • \lVert x \mapsto \sigma(W_n \cdots \sigma(W_1 x)) \rVert_L ≪ \lVert W_n \rVert_\text{op} \cdots \lVert W_1 \rVert_\text{op}

Continuity theorem proof

  • k_\psic(x, y) = \ktop(\phi_\psic(x), \phi(y)) means \small d_\psic(x, y) = \lVert k_\psic(x, \cdot) - k_\psic(y, \cdot) \rVert_{\h_{k_\psic}} \le L_{\ktop} \lVert \phi_\psic \rVert_\lip \lVert x - y \rVert
  • Can show \mmd_\psic \le \W_{d_\psic} \le L_{\ktop} \lVert \phi_\psic \rVert_\lip \W
  • By assumption on \ktop , \sigma_{\SS,k,\lambda}^{-2} \ge \gamma_{\ktop}^2 \E[\lVert \nabla \phi_\psic(\Xtilde) \rVert_F^2]
  • \smmd^2 \le \frac{L_{\ktop}^2 \lVert \phi_\psic \rVert_\lip^2}{\gamma_{\ktop}^2 \E{\lVert \nabla_{\Xtilde} \phi_\psic(\Xtilde) \rVert_F^2}} \W \fragment[5]{\le \frac{L_{\ktop}^2 \kappa^L}{\gamma_{\ktop}^2 d_\mathrm{top} \alpha^L} \W}
  • Because Leaky-ReLU, \phi_\psic(X) = \alpha(\psic) \phi_{\bar\psic}(X) , \lVert \phi_{\bar\psic} \rVert_\lip \le 1
  • For Lebesgue-almost all \Xtilde , \lVert \nabla_\Xtilde \phi_{\bar\psic}(\Xtilde) \rVert_F^2 \ge \frac{d_\mathrm{top} \alpha^L}{\kappa^L}

\D_\mathrm{SMMD} : 2d example

Target \PP and model \Qtheta samples
Kernels from \mathrm{SMMD}_{\PP, k, \lambda} , early in optimization
Kernels from \mathrm{MMD}_{k} (early)
Critic gradients from \mathrm{SMMD}_{\PP, k, \lambda} (early)
Critic gradients from \mathrm{MMD}_{k} (early)
Kernels from \mathrm{SMMD}_{\PP, k, \lambda} , late in optimization
Kernels from \mathrm{MMD}_{k} (late)
Critic gradients from \mathrm{SMMD}_{\PP, k, \lambda} (late)
Critic gradients from \mathrm{MMD}_{k} (late)

Model on 160 \times 160 CelebA

SN-SMMD-GAN
KID: 0.006
WGAN-GP
KID: 0.022

Implicit generative model evaluation

  • No likelihoods, so…how to compare models?
  • Main approach:
    look at a bunch of pictures and see if they're pretty or not
    • Easy to find (really) bad samples
    • Hard to see if modes are missing / have wrong probabilities
    • Hard to compare models beyond certain threshold
  • Need better, quantitative methods
  • Our method: Kernel Inception Distance (KID)

Inception score [Salimans+ NIPS-16]

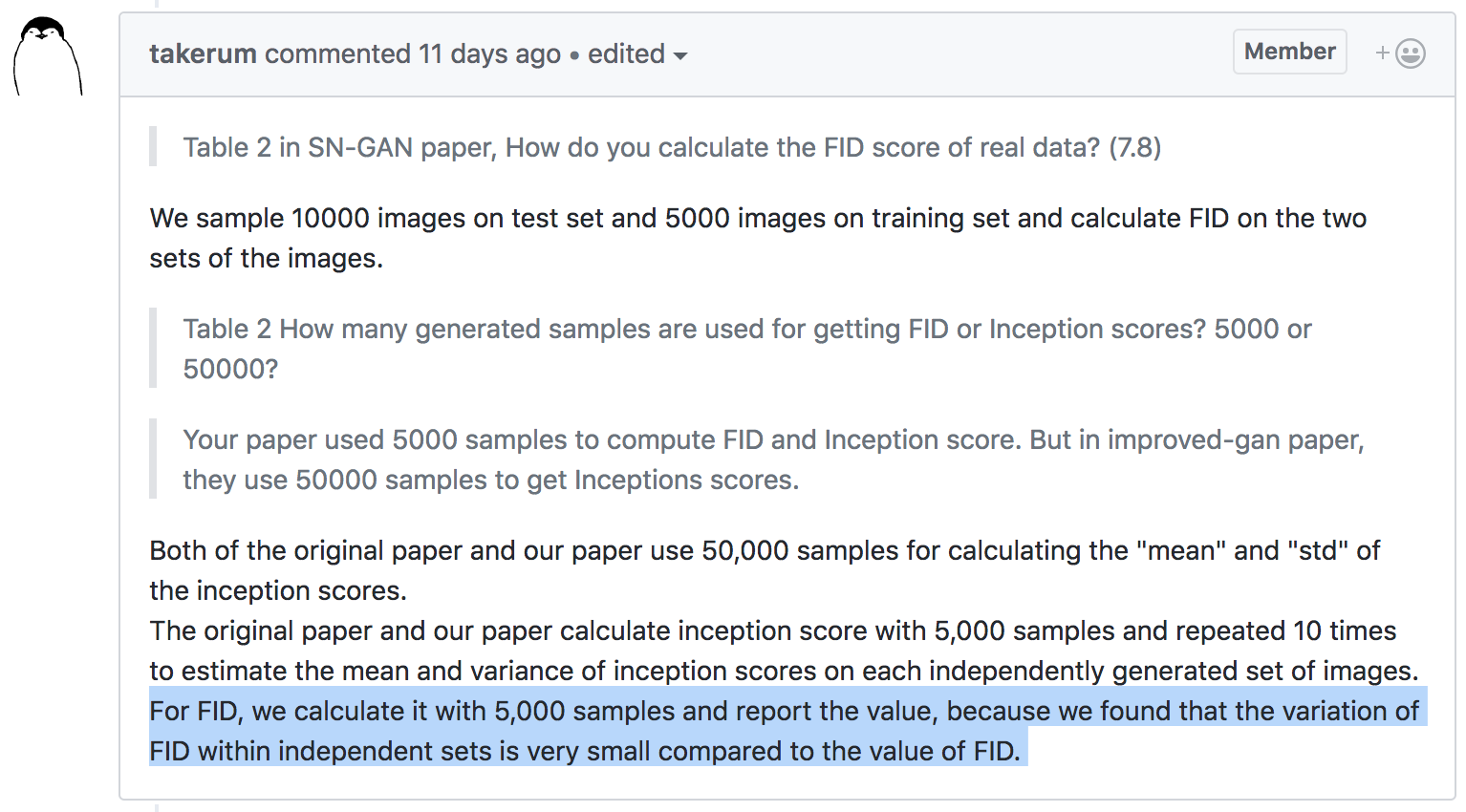
  • Previously standard quantitative method
  • Based on ImageNet classifier label predictions
    • Classifier should be confident on individual images
    • Predicted labels should be diverse across sample
  • No notion of target distribution \Pdata
  • Scores completely meaningless on LSUN, Celeb-A, SVHN, …
  • Not great on CIFAR-10 either

Fréchet Inception Distance (FID) [Heusel+ NIPS-17]

  • Fit normals to Inception hidden layer activations of \PP and \QQ
  • Compute Fréchet (Wasserstein-2) distance between fits
  • Meaningful on not-ImageNet datasets
  • Estimator extremely biased, tiny variance
  • \operatorname{FID}(\PP_1, \QQ) < \operatorname{FID}(\PP_2, \QQ) , \E \operatorname{FID}(\hat \PP_1, \QQ) > \E \operatorname{FID}(\hat \PP_2, \QQ)

New method: Kernel Inception Distance (KID)

Automatic learning rate adaptation with KID

  • Models need appropriate learning rate schedule to work well
  • Automate with three-sample MMD test [Bounliphone+ ICLR-16]:

Training process on CelebA

image/svg+xml

Controlling critic complexity

Model on 64 \times 64 ImageNet

SN-SMMDGAN

KID: 0.035
SN-GAN

KID: 0.044
BGAN

KID: 0.047

Recap

  • Can train generative models by minimizing a flexible, smooth distance between distributions
  • Combine kernels with gradient penalties
  • Strong practical results, some understanding of theory
Demystifying MMD GANs
Bińkowski*, Sutherland*, Arbel, and Gretton
ICLR 2018
On Gradient Regularizers for MMD GANs
Arbel*, Sutherland*, Bińkowski, and Gretton
NeurIPS 2018

Links + code: see djsutherland.ml. Thanks!

Learning deep kernels for exponential family densities
Wenliang*, Sutherland*, Strathmann, and Gretton
ICML 2019