\definecolor{cb1}{RGB}{76,114,176} \definecolor{cb2}{RGB}{221,132,82} \definecolor{cb3}{RGB}{85,168,104} \definecolor{cb4}{RGB}{196,78,82} \definecolor{cb5}{RGB}{129,114,179} \definecolor{cb6}{RGB}{147,120,96} \definecolor{cb7}{RGB}{218,139,195} \newcommand{\abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\norm}[1]{\left\lVert #1 \right\rVert} \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator{\bigO}{\mathcal{O}} \DeclareMathOperator{\Cov}{Cov} \DeclareMathOperator{\E}{\mathbb{E}} \newcommand{\indic}{\mathbb{I}} \newcommand{\R}{\mathbb{R}} \newcommand{\tp}{^\mathsf{T}} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Var}{Var} \DeclareMathOperator{\NTK}{NTK} \DeclareMathOperator{\eNTK}{eNTK} \DeclareMathOperator{\pNTK}{pNTK} \newcommand{\lin}{\mathit{lin}} \newcommand{\xt}{{\color{cb2} \tilde x}} \newcommand{\exi}{{\color{cb1} x_i}} \newcommand{\yi}{{\color{cb1} y_i}} \newcommand{\Xs}{{\color{cb1} \mathbf X}} \newcommand{\ys}{{\color{cb1} \mathbf y}} \newcommand{\w}{\mathbf{w}} \newcommand{\tar}{\mathit{tar}} \newcommand{\ptari}{{\color{cb1} p^\tar_i}} \newcommand{\pstari}{{\color{cb1} p^*_i}}

In Defence of (Empirical) Neural Tangent Kernels

Danica J. Sutherland(she)
University of British Columbia (UBC) / Alberta Machine Intelligence Institute (Amii)
“Zig-zagging” [ICLR-22]
Yi Ren
Shangmin Guo
Finetuning [ICLR-23]
Yi Ren
Shangmin Guo
Wonho Bae
Active learning [NeurIPS-22]
Mohamad Amin Mohamadi
Wonho Bae
Pseudo-NTK [new!]
Mohamad Amin Mohamadi
Wonho Bae

MSR Montréal / Mila - March 21, 2023

(Swipe or arrow keys to move through slides; m for a menu to jump; ? to show more.)

One path to NTKs(Taylor's version)

  • “Learning path” of a model's predictions: f_t(\xt) for some fixed \xt as params \w_t change
  • Let's start with “plain” SGD on \frac1N \sum_{i=1}^N \ell_{\yi}(f(\exi)) :

    • \begin{align*} \!\!\!\!\!\!\!\!\!\!\! \underbrace{f_{t+1}(\xt) - f_t(\xt)}_{k \times 1} &= \underbrace{\left( \nabla_\w f(\exi) \rvert_{\w_t} \right)}_{k \times p} \, \underbrace{(w_{t+1} - w_t)}_{p \times 1} {\color{gray}{} + \bigO\left( \norm{\w_{t+1} - \w_t}^2 \right)} \\&\fragment[3]{ {} = \left( \nabla_\w f(\xt) \rvert_{\w_t} \right) \left( - \eta \nabla_\w \ell_\yi(f(\exi)) \rvert_{\w_t} \right)\tp {\color{gray}{} + \bigO(\eta^2)} } \\&\fragment[4]{ {} = - \eta \, \underbrace{ \left( \nabla_\w f(\xt) \rvert_{\w_t} \right) }_{k \times p} \, \underbrace{ \left( \nabla_\w f(\exi) \rvert_{\w_t} \right)\tp }_{p \times k} \, \underbrace{ \ell_\yi'(f_t(\exi)) }_{k \times 1} {\color{gray}{} + \bigO(\eta^2)} } \\&\fragment[5]{ {} = - \eta \eNTK_{\w_t}(\xt, \exi) \, \ell'_\yi(f_t(\exi)) {\color{gray}{} + \bigO(\eta^2)} } \end{align*}

  • Defined \eNTK_\w(\xt, \exi) = \left( \nabla_\w f(\xt; \w) \right) \, \left( \nabla_\w f(\exi; \w) \right)\tp \in \R^{k \times k}
    • (\exi, \yi) step barely changes \xt prediction if \eNTK_{\w_t}(\xt, \exi) is small
  • \ell_y'(\hat y) = \hat y - y for square loss, \hat y_y - \log \sum_{j=1}^k \exp(\hat y_j) for cross-entropy
  • Full-batch GD: “stacking things up”, \begin{align*} f_{t+1}(\xt) - f_t(\xt) &= - \frac{\eta}{N} \sum_{i=1}^N \eNTK_{\w_t}(\xt, \exi) \ell'_{\yi}(f_t(\exi)) {\color{gray}{} + \bigO(\eta^2)} \\&\fragment[1]{ {} = - \frac{\eta}{N} \underbrace{\eNTK_{\w_t}(\xt, \Xs)}_{k \times k N} \, \underbrace{L_\ys'(f_t(\Xs))}_{k N \times 1} {\color{gray}{} + \bigO(\eta^2)} } \end{align*}
  • Observation I: If f is “wide enough” with any usual architecture+init* [Yang+Litwin 2021], \eNTK(\cdot, \Xs) is roughly constant through training
    • For square loss, L'_{\yi}(f_t(\Xs)) = f_t(\Xs) - \yi : dynamics agree with kernel regression!
    • f_t(\xt) \xrightarrow{t \to \infty} \eNTK_{\w_0}(\xt, \Xs) \eNTK_{\w_0}(\Xs, \Xs)^{-1} (\ys - f_0(\Xs)) + f_0(\xt)
  • Observation II: As f becomes “infinitely wide” with any usual architecture+init* [Yang 2019], \eNTK_{\w_0}(x_1, x_2) \xrightarrow{a.s.} \NTK(x_1, x_2) , independent of the random \w_0

Infinite NTKs are great

  • Infinitely-wide neural networks have very simple behaviour!
    • No need to worry about bad local minima, optimization complications, …
    • Understanding “implicit bias” of wide nets \approx understanding NTK norm of functions
  • Can compute \NTK exactly for many architectures
  • A great kernel for many kernel methods!

But (infinite) NTKs aren't “the answer”

  • Computational expense:
    • Poor scaling for large-data problems: typically n^2 memory and n^2 to n^3 computation
      • CIFAR-10 has n = 50\,000 , k = 10 : an nk \times nk matrix of float64s is 2 terabytes!
      • ILSVRC2012 has n \approx 1\,200\,000 , k = 1\,000 : 11.5 million terabytes (exabytes)
    • For deep/complex models (especially CNNs), each pair very slow / memory-intensive
  • Practical performance:
    • Typically performs worse than GD for “non-small-data” tasks (MNIST and up)
  • Theoretical limitations:
    • NTK “doesn't do feature learning”:
    • We now know many problems where gradient descent on an NN \gg any kernel method
      • Cases where GD error \to 0 , any kernel is barely better than random [Malach+ 2021]

What can we learn from empirical NTKs?

In this talk:

  • As a theoretical-ish tool for local understanding:
    • Fine-grained explanation for early stopping in knowledge distillation
    • How you should fine-tune models
  • As a practical tool for approximating “lookahead” in active learning
  • Plus: efficiently approximating \eNTK s for large output dimensions k , with guarantees

Better supervisory signal implies better learning

  • Classification: target is L_P(f) = \E_{(x, y)} \ell(f(x), y) = \E_x \E_{y \mid x} \ell(f(x), y)
  • Normally: see \{(\exi, \yi)\} , minimize ( \vec\ell(\hat y) \in \R^k is vector of losses for all possible labels) \!\!\! L(f) = \frac1N \sum_{i=1}^N \ell(f(\exi), \yi) \fragment[1]{= \frac1N \sum_{i=1}^N \sum_{c=1}^k \indic(\yi = c) \ell(f(\exi), c) } \fragment[2]{= \frac1N \sum_{i=1}^n e_{\yi} \cdot \vec\ell(f(\exi))}
  • Potentially better scheme: see \{(\exi, \ptari)\} , minimize \displaystyle L^\tar(f) = \frac1N \sum_{i=1}^N \ptari \cdot \vec\ell(f(\exi))
    • Can reduce variance if \ptari \approx \pstari , the true conditional probabilities

Knowledge distillation

  • Process:
    • Train a teacher f^\mathit{teacher} on \{ (\exi, \yi) \} with standard ERM, L(f)
    • Train a student on \{ (\exi, {\color{cb4} f^\mathit{teacher}}(\exi)) \} with L^\tar
  • Usually \color{cb5} f^\mathit{student} is “smaller” than \color{cb4} f^\mathit{teacher}
  • But “self-distillation” (using the same architecture), often \color{cb5} f^\mathit{student} outperforms \color{cb4} f^\mathit{teacher} !
  • One possible explanation: \color{cb4} f^\mathit{teacher}(\exi) is closer to \pstari than sampled \yi
  • But why would that be?

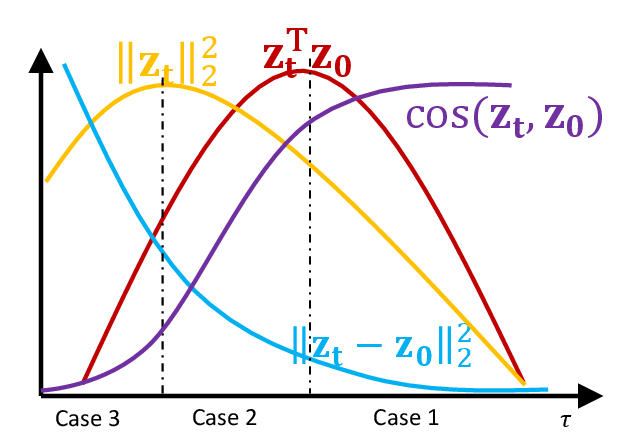
Zig-Zagging behaviour in learning

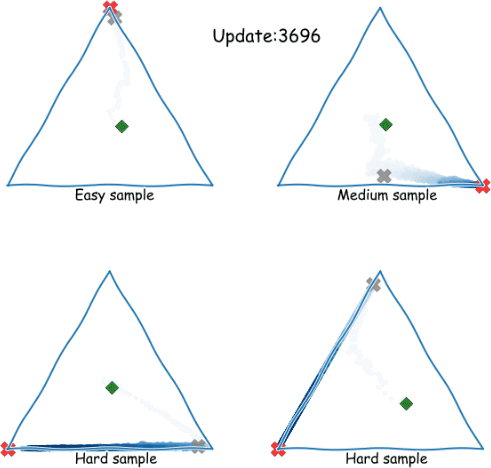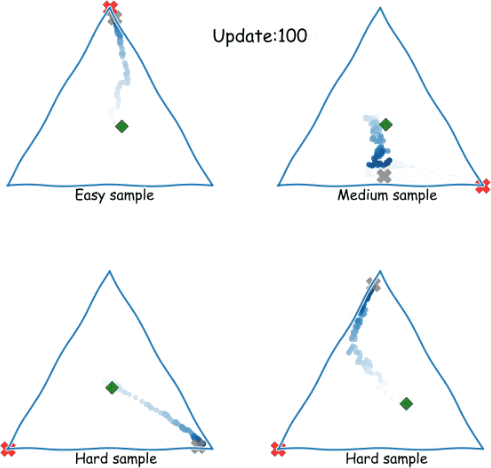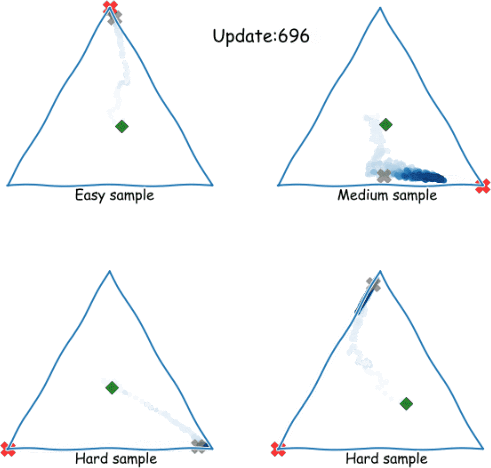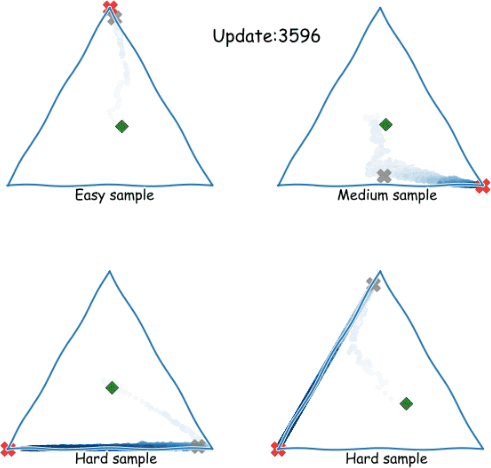
Plots of (three-way) probabilistic predictions: \boldsymbol\times shows \pstari , \boldsymbol\times shows \yi

eNTK explains it

  • Let q_t(\xt) = \operatorname{softmax}(f_t(\xt)) \in \R^k ; for cross-entropy loss, one SGD step gives us q_{t+1}(\xt) - q_t(\xt) = \eta \; \mathcal A_t(\xt) \, \eNTK_{\w_t}(\xt, \exi) \, (\ptari - q_t(\exi)) {\color{gray}{} + \bigO(\eta^2)} \mathcal A_t(\xt) = \operatorname{diag}(q_t(\xt)) - q_t(\xt) q_t(\xt)\tp is the covariance of a \operatorname{Categorical}(q_t(\xt))
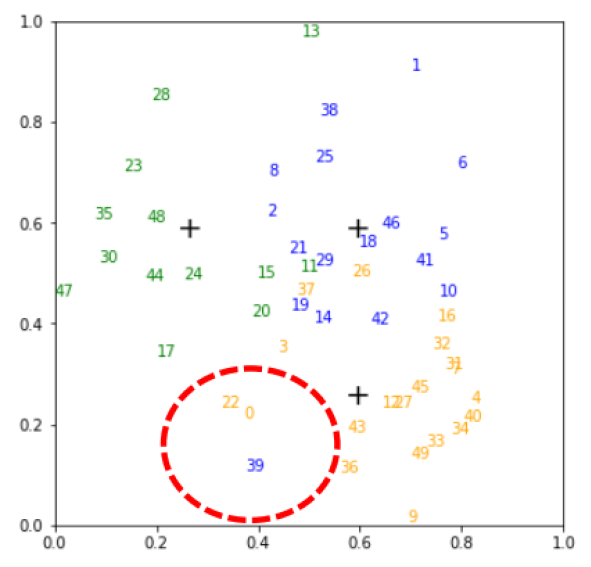
  • Improves distillation (esp. with noisy labels) to take moving average of q_t(\exi) as \ptari

What can we learn from empirical NTKs?

In this talk:

  • As a theoretical-ish tool for local understanding:
    • Fine-grained explanation for early stopping in knowledge distillation
    • How you should fine-tune models
  • As a practical tool for approximating “lookahead” in active learning
  • Plus: efficiently approximating \eNTK s for large output dimensions k , with guarantees

Fine-tuning

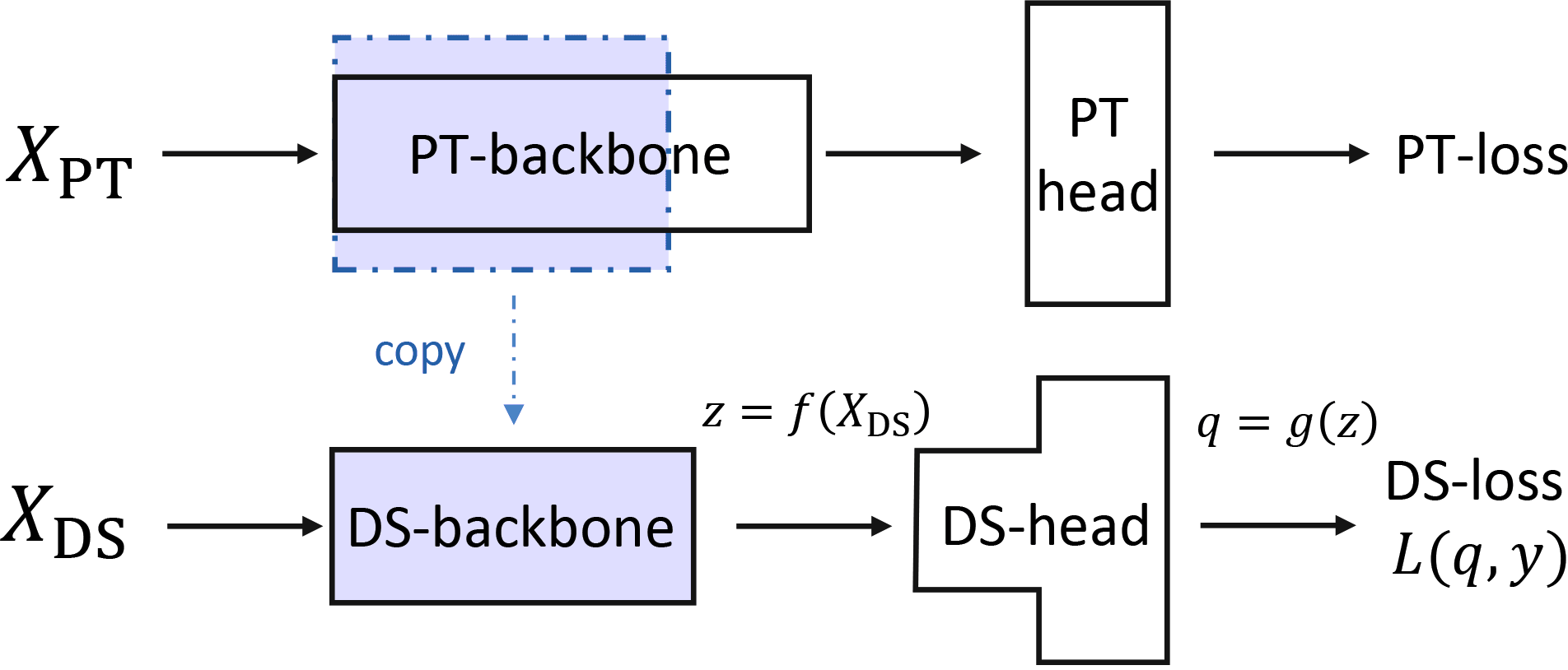
  • Pretrain, re-initialize a random head, then adapt to a downstream task. Two phases:
    • Head probing: only update the head g(z)
    • Fine-tuning: update head g(z) and backbone z = f(x) together
  • If we only fine-tune: noise from random head might break our features!
  • If we head-probe to convergence: might already fit training data and not change features!

How much do we change our features?

  • Same kind of decomposition with backbone features z = f(x) , head q = \operatorname{softmax}(g(z)) : z_{t+1}(\xt) - z_t(\xt) = \frac{\eta}{N} \sum_{i=1}^N \underbrace{\eNTK_{\w_t}^{f}(\xt, \exi)}_\text{eNTK of backbone} \, \underbrace{\left(\nabla_z q_t(\exi)\right)\tp_\phantom{\w_t}\!\!\!}_\text{direction of head} \, \underbrace{(e_{\yi} - q_t(\exi))_\phantom{\w_t}\!\!\!\!\!\!\!}_\text{“energy"} {\color{gray}{} + \bigO(\eta^2)}
  • If initial “energy”, e.g. \E_{\exi,\yi} \norm{e_{\yi} - p_0(\exi)} , is small, features don't change much
  • If we didn't do any head probing, “direction” is very random, especially if g is rich
  • Specializing to simple linear-linear model, can get insights about trends in z
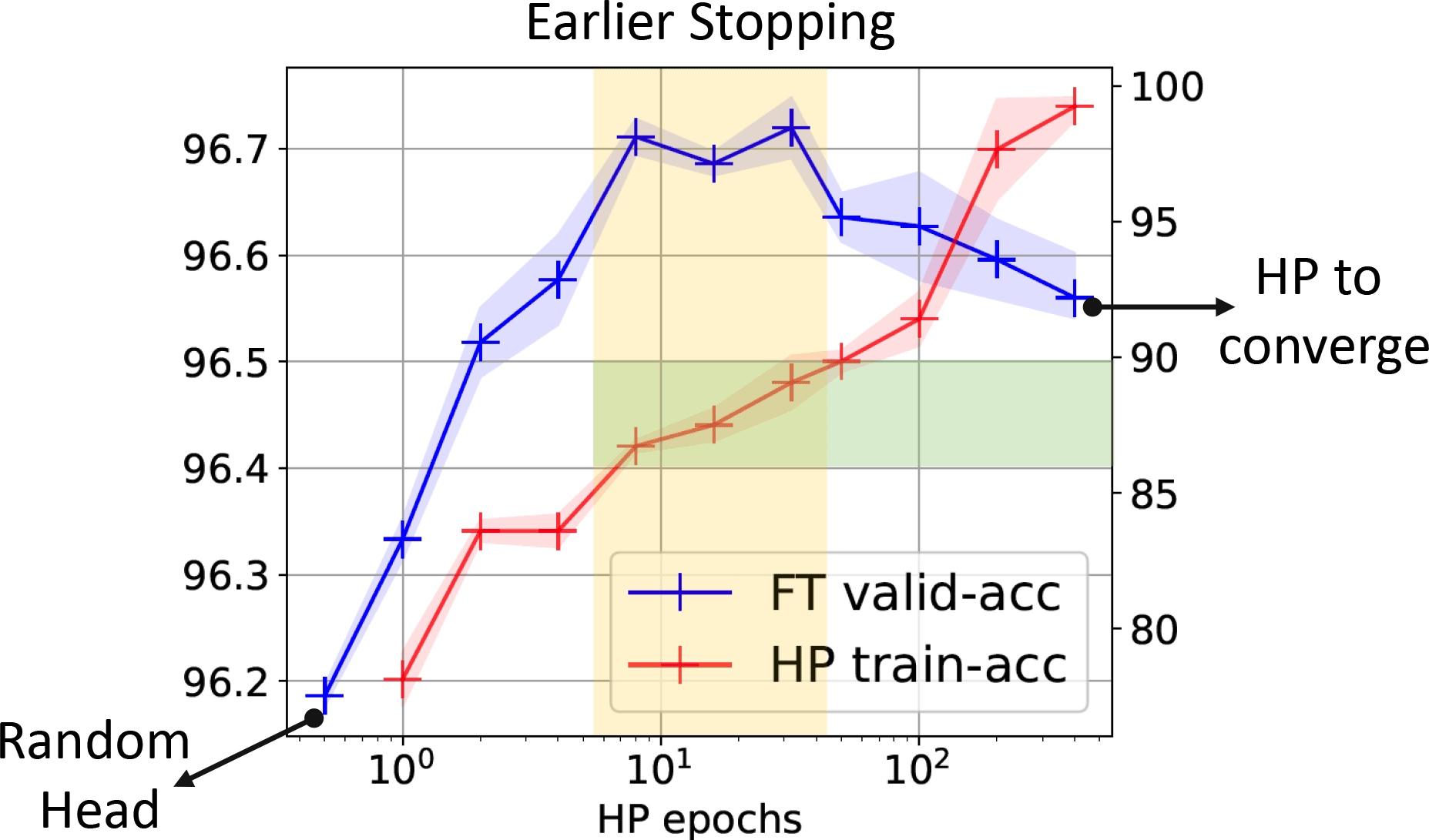
  • Recommendations from paper:
    • Early stop during head probing (ideally, try multiple lengths for downstream task)
    • Label smoothing can help; so can more complex heads, but be careful

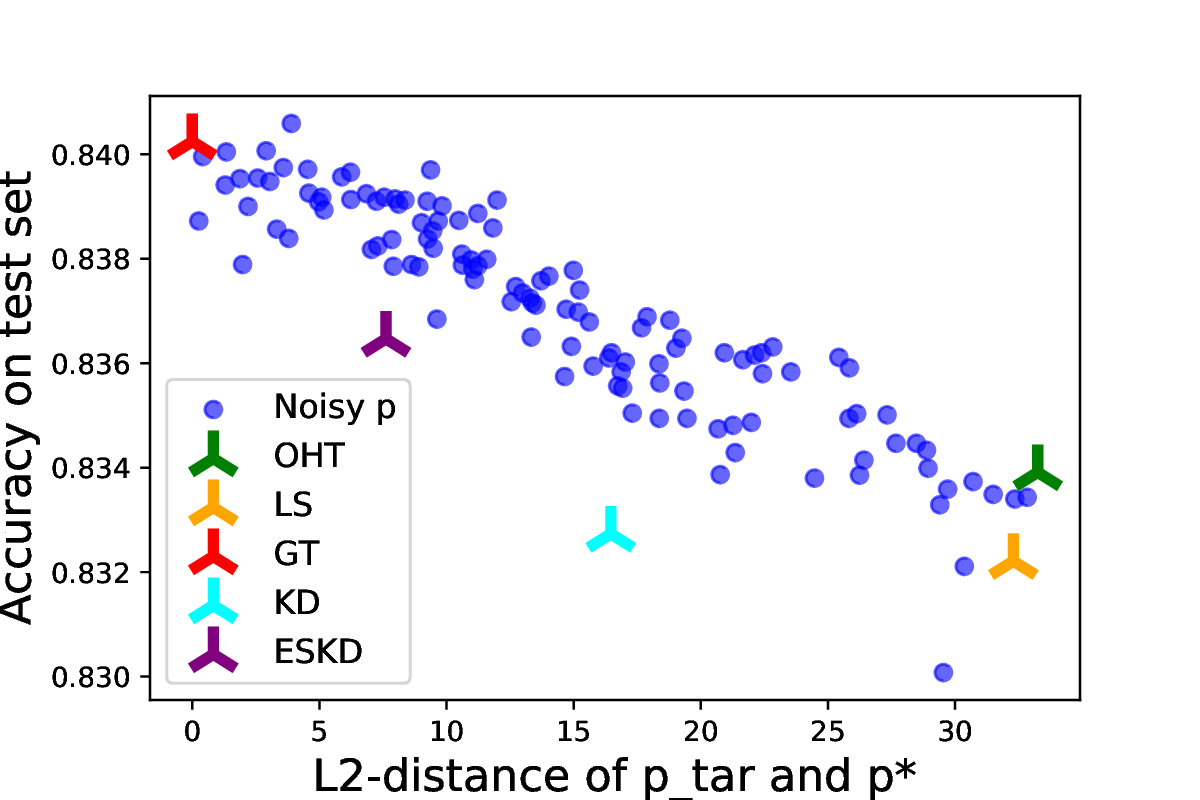
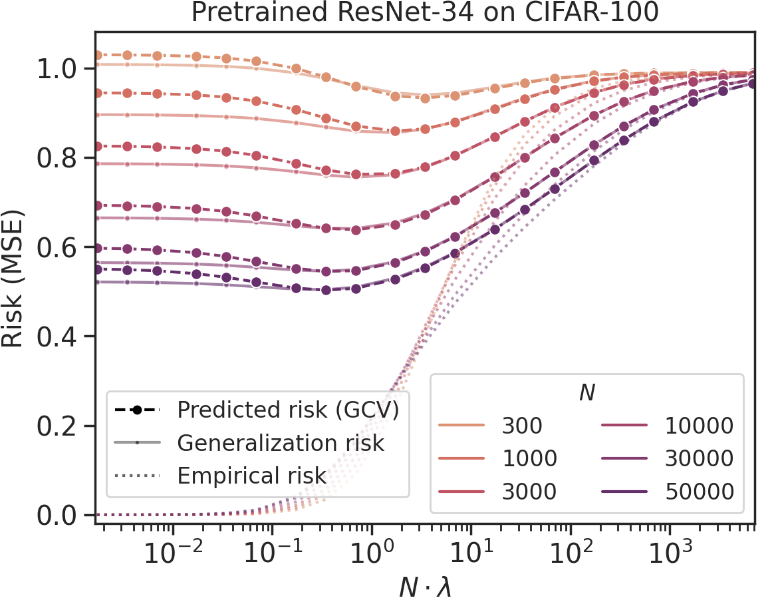
How good will our fine-tuned features be? [Wei/Hu/Steinhardt 2022]

  • With random head (no head probing),
    generalized cross-validation on eNTK model gives excellent estimate of downstream loss

What can we learn from empirical NTKs?

In this talk:

  • As a theoretical-ish tool for local understanding:
    • Fine-grained explanation for early stopping in knowledge distillation
    • How you should fine-tune models
  • As a practical tool for approximating “lookahead” in active learning
  • Plus: efficiently approximating \eNTK s for large output dimensions k , with guarantees

Pool-based active learning

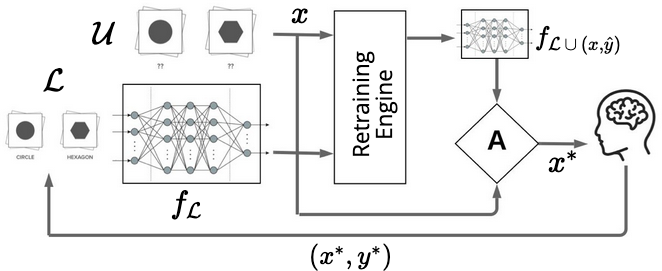
  • Pool of unlabeled data available; ask for annotations of the “most informative” points
  • Kinds of acquisition functions used for deep active learning:
    • Uncertainty-based: maximum entropy, BALD
    • Representation-based: BADGE, LL4AL
  • Another kind used for simpler models: lookahead criteria
    • “How much would my model change if I saw \exi with label \yi ?”
    • Too expensive for deep learning…unless you use a local approximation to retraining

Approximate retraining with local linearization

  • Given f_{\mathcal L} trained on labeled data \mathcal L , approximate f_{\mathcal L \cup \{(\exi, \yi)\}} with local linearization \!\!\!\!\! f_{\mathcal L \cup \{(\exi, \yi)\}}(\xt) \approx f_{\mathcal L}(\xt) + \eNTK_{\w_{\mathcal L}}\left(\xt, \begin{bmatrix} \Xs_{\mathcal L} \\ \exi \end{bmatrix} \right) \eNTK_{\w_{\mathcal L}}\left(\begin{bmatrix} \Xs_{\mathcal L} \\ \exi \end{bmatrix}, \begin{bmatrix} \Xs_{\mathcal L} \\ \exi \end{bmatrix} \right)^{-1} \left( \begin{bmatrix} \ys_{\mathcal L} \\ \yi \end{bmatrix} - f_{\mathcal L}\left(\begin{bmatrix} \Xs_{\mathcal L} \\ \exi \end{bmatrix} \right) \right)
    • Rank-one updates for efficient computation: schema
  • We prove this is exact for infinitely wide networks
    • f_0 \to f_{\mathcal L} \to f_{\mathcal L \cup \{(\exi, \yi)\}} agrees with direct f_0 \to f_{\mathcal L \cup \{(\exi, \yi)\}}
  • Local approximation with eNTK “should” work much more broadly than “NTK regime”

Much faster than SGD

Much more effective than infinite NTK and one-step SGD

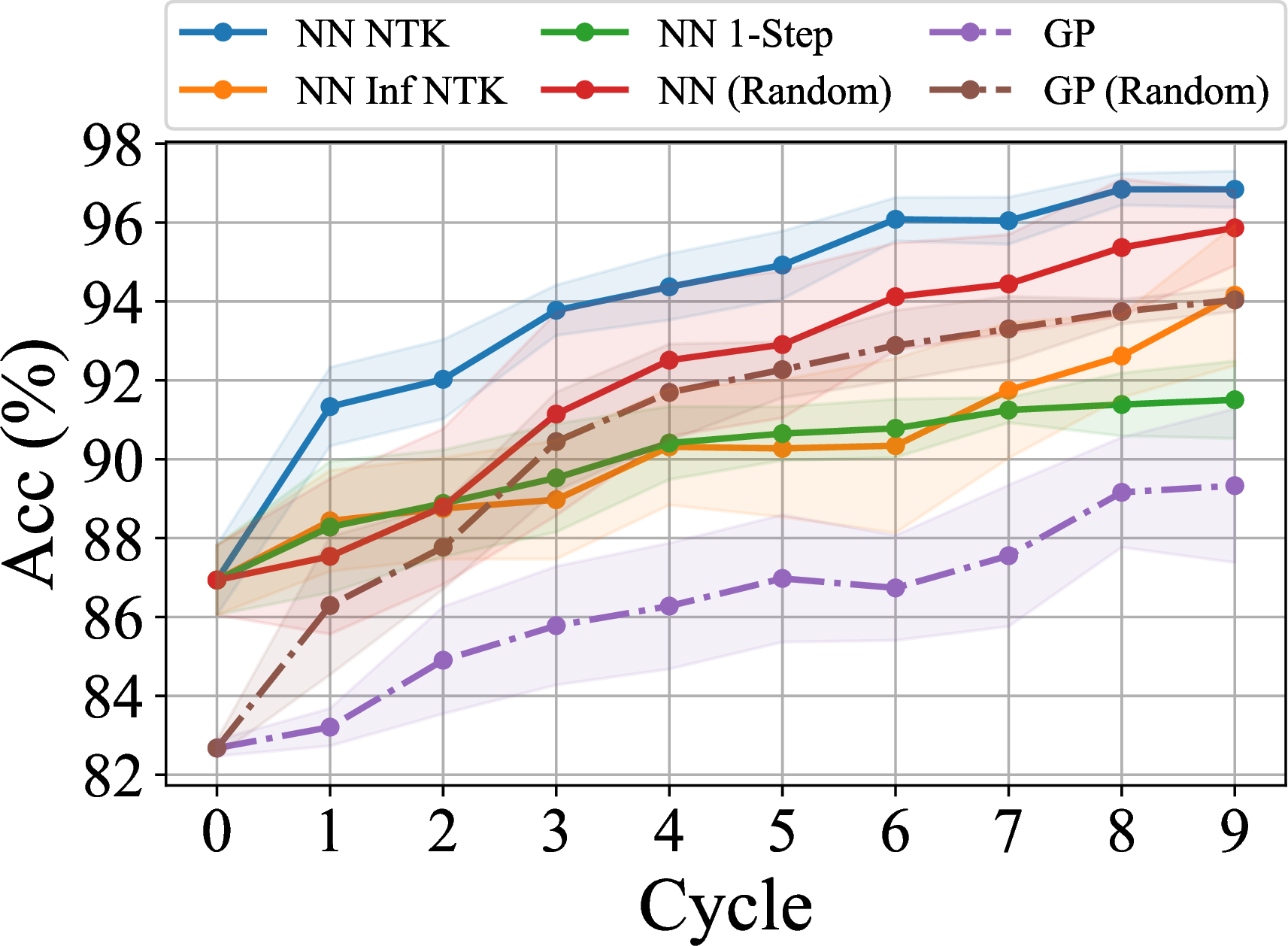
Matches/beats state of the art

Downside: usually more computationally expensive (especially memory)

Enables new interaction modes

  • “Sequential” querying: incorporate true new labels one-at-a-time instead of batch
    • Only update \eNTK occasionally
    • Makes sense when labels cost $ but are fast; other deep AL methods need to retrain

What can we learn from empirical NTKs?

In this talk:

  • As a theoretical-ish tool for local understanding:
    • Fine-grained explanation for early stopping in knowledge distillation
    • How you should fine-tune models
  • As a practical tool for approximating “lookahead” in active learning
  • Plus: efficiently approximating \eNTK s for large output dimensions k , with guarantees

Approximating empirical NTKs

  • I hid something from you on active learning (and Wei/Hu/Steinhardt fine-tuning) results…
  • With k classes, \eNTK(\Xs, \Xs) \in \R^{k N \times k N} – potentially very big
  • But actually, we know that \E_{\w} \eNTK_\w(x_1, x_2) is diagonal for most architectures
    • Let \displaystyle \pNTK_\w(x_1, x_2) = \underbrace{\left[ \nabla_\w f_1(x_1) \right] }_{1 \times p} \underbrace{\left[ \nabla_\w f_1(x_2) \right) \tp}_{p \times 1} % \underbrace{\left[ \nabla_\w\left( \frac{1}{\sqrt k} \sum_{j=1}^k f_j(x_1) \right) \right]}_{1 \times p} % \underbrace{\left[ \nabla_\w\left( \frac{1}{\sqrt k} \sum_{j=1}^k f_j(x_2) \right) \right]\tp}_{p \times 1} . \E_\w \eNTK_\w(x_1, x_2) = \E_w\left[ \pNTK_\w(x_1, x_2) \right] I_k .       \pNTK(\Xs, \Xs) \in \R^{N \times N} (no k !)
    • Can also use “sum of logits” \frac{1}{\sqrt k} \sum_{j=1}^k f_j instead of just “first logit” f_1
  • Lots of work (including above) has used \pNTK instead of \eNTK
    • Often without saying anything; sometimes doesn't seem like they know they're doing it
  • Can we justify this more rigorously?

pNTK motivation

  • Say f(x) = V \phi(x) , \phi(x) \in \R^h , and V \in \R^{k \times h} has rows v_j \in \R^h with iid entries
  • If v_{j,i} \sim \mathcal N(0, \sigma^2) , then v_1 and \frac{1}{\sqrt k} \sum_{j=1}^k v_j have same distribution \begin{align*} \fragment[1]{ \eNTK_\w(x_1, x_2)_{jj'} }&\fragment[1]{ {} = v_j\tp \eNTK^\phi_{\w \setminus V}(x_1, x_2) \, v_{j'} + \indic(j = j') \phi(x_1)\tp \phi(x_2) } \\ \fragment[2]{\pNTK_\w(x_1, x_2)} &\fragment[2]{ {} = {\color{cb4} v_1\tp} \eNTK^\phi_{\w \setminus V}(x_1, x_2) \, {\color{cb4} v_1} + \phi(x_1)\tp \phi(x_2) } \end{align*}
  • We want to bound difference \eNTK(x_1, x_2) - \pNTK(x_1, x_2) I_k
    • Want v_1\tp A v_1 and v_j\tp A v_j to be close, and v_j\tp A v_{j'} small, for random v and fixed A
    • Using Hanson-Wright: \displaystyle \frac{\norm{\eNTK - \pNTK I}_F}{\norm{\eNTK}_F} \le \frac{\norm{\eNTK^\phi}_F + 4 \sqrt h}{\Tr(\eNTK^\phi)} k \log \frac{2 k^2}{\delta}
    • Fully-connected ReLU nets at init., fan-in mode: numerator \bigO(h \sqrt h) , denom \Theta(h^2)

pNTK's Frobenius error

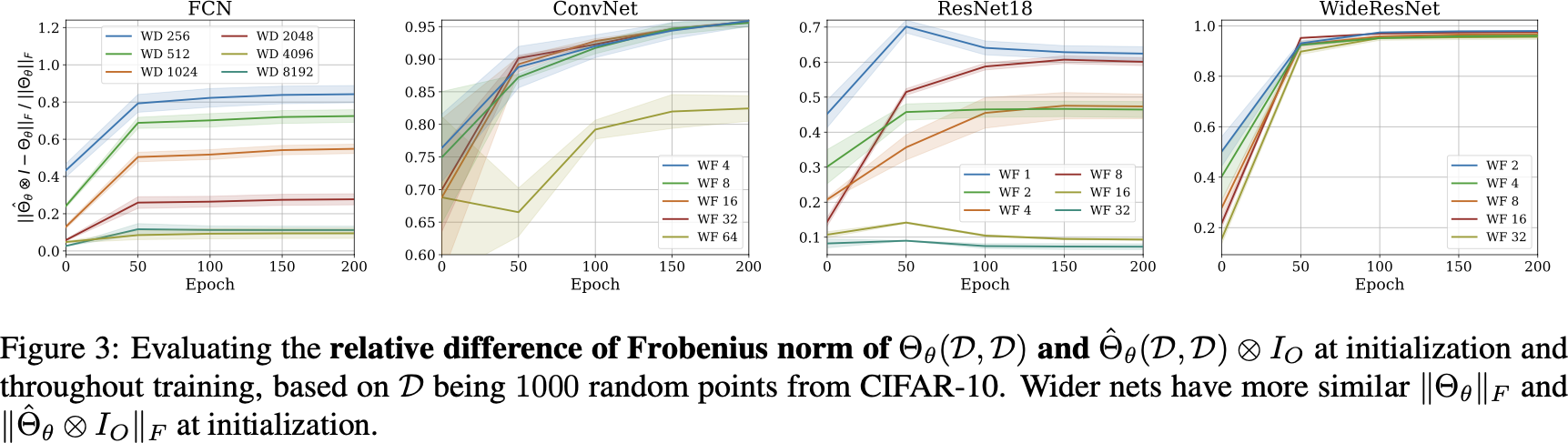
Same kind of theorem / empirical results for largest eigenvalue,
and empirical results for \lambda_\min , condition number

Kernel regression with pNTK

  • Reshape things to handle prediction appropriately: \begin{align*} \underbrace{f_{\eNTK}(\xt)}_{k \times 1} &= \underbrace{f_0(\xt)}_{k \times 1} + \phantom{\Big(} \underbrace{\eNTK_{\w_0}(\xt, \Xs)}_{k \times k N} \,\underbrace{\eNTK_{\w_0}(\Xs, \Xs)^{-1}}_{k N \times k N} \,\underbrace{(\ys - f_0(\Xs))}_{kN \times 1} \\ \underbrace{f_{\pNTK}(\xt)}_{k \times 1} &= \underbrace{f_0(\xt)}_{k \times 1} + \Big( \underbrace{\pNTK_{\w_0}(\xt, \Xs)}_{1 \times N} \,\underbrace{\pNTK_{\w_0}(\Xs, \Xs)^{-1}}_{N \times N} \,\underbrace{(\ys - f_0(\Xs))}_{N \times k} \Big)\tp \end{align*}
  • We have \norm{f_{\eNTK}(\xt) - f_{\pNTK}(\xt)} = \bigO(\frac{1}{\sqrt h}) again
    • If we add regularization, need to “scale” \lambda between the two

Kernel regression with pNTK

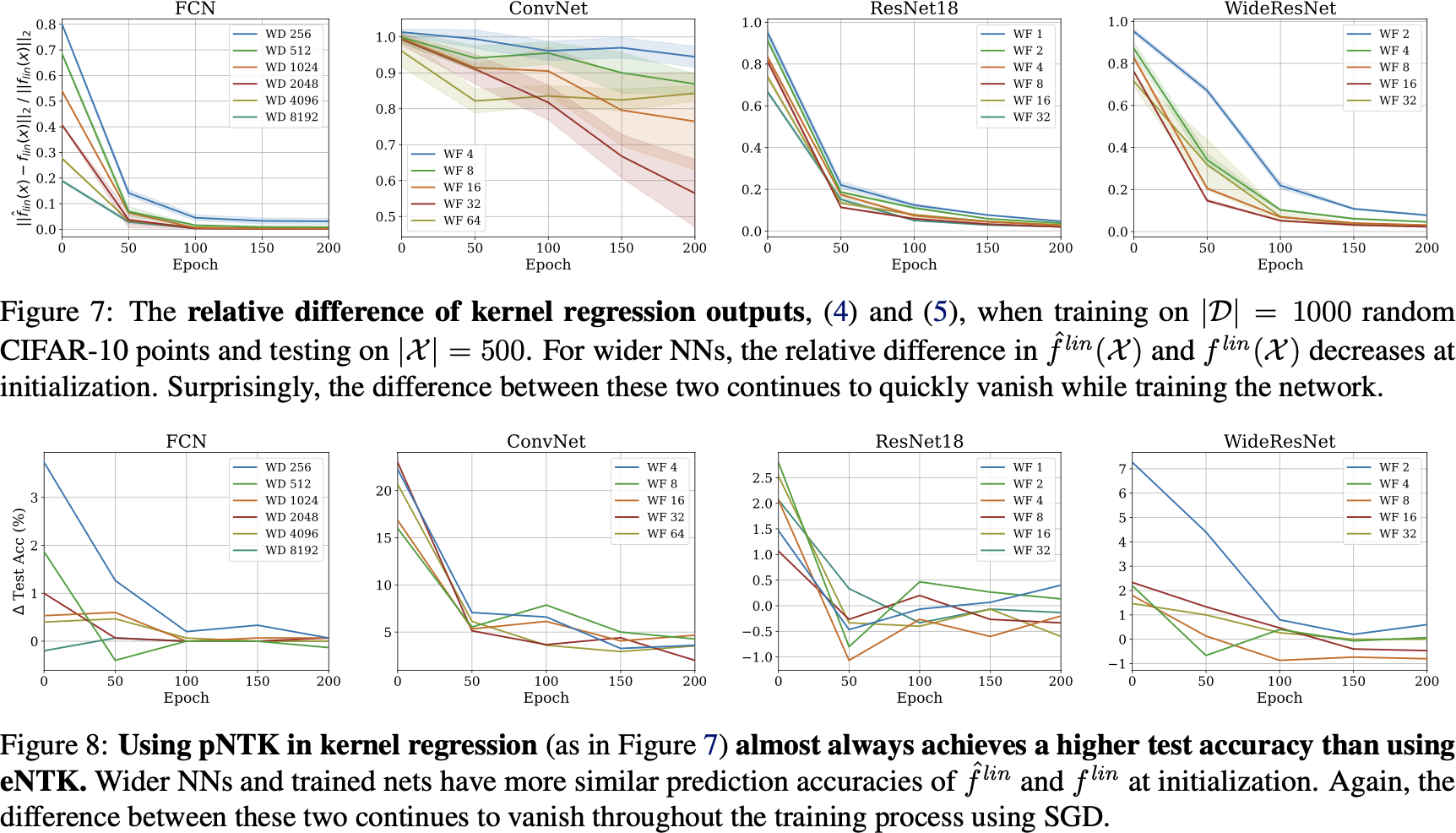
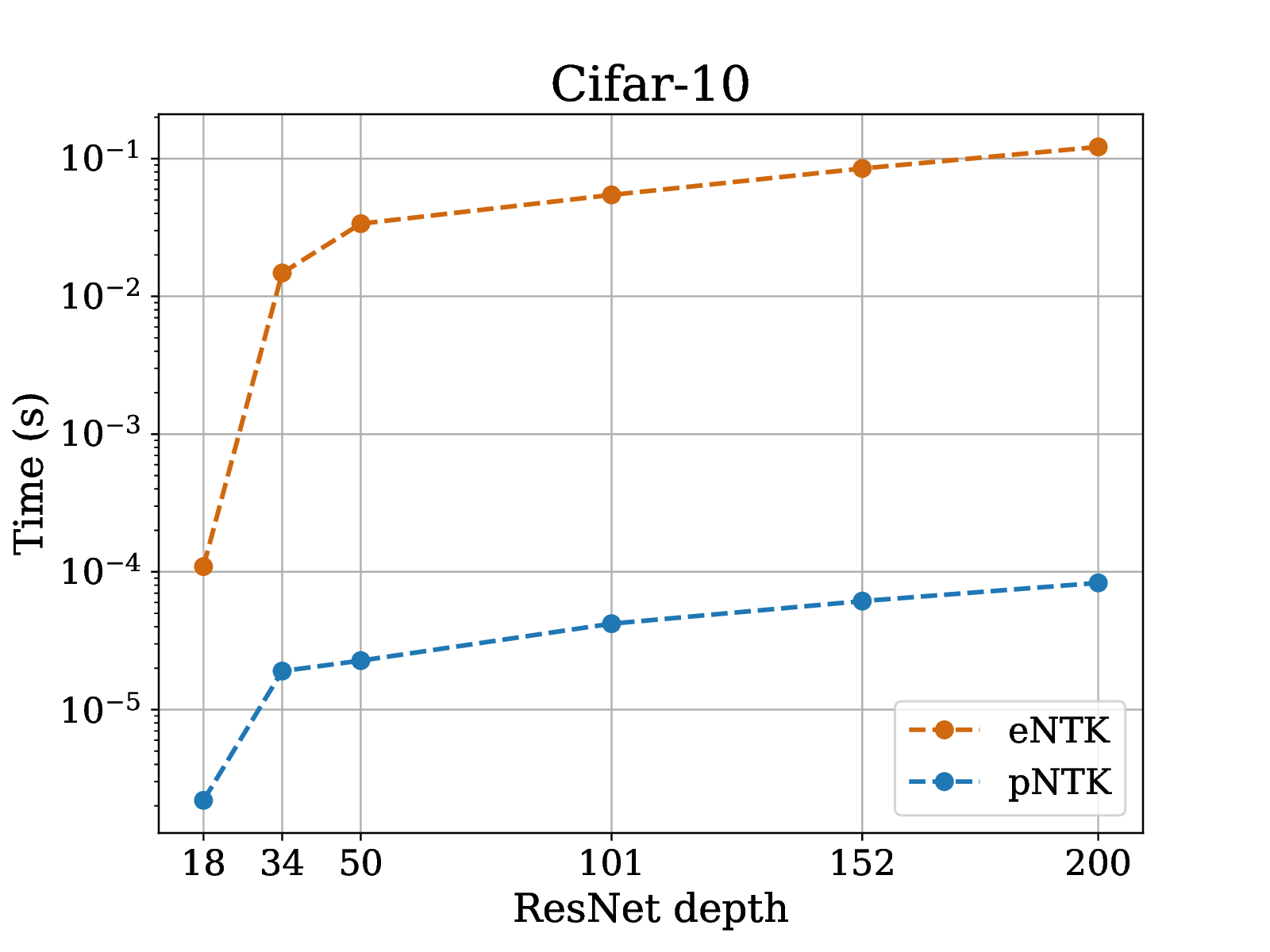
pNTK speed-up

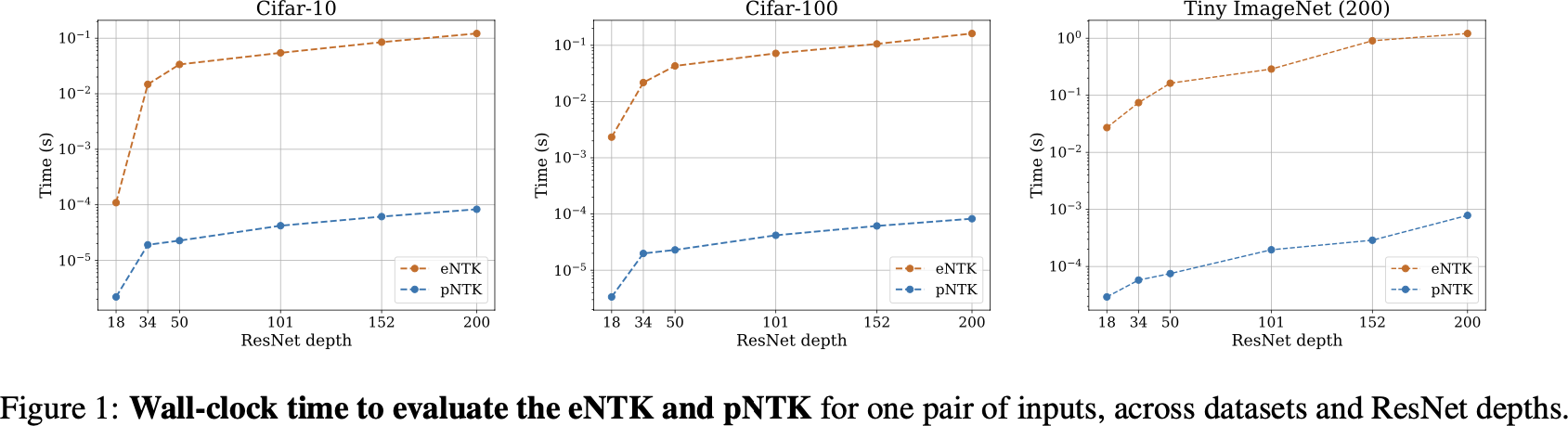
pNTK speed-up on active learning task

pNTK for full CIFAR-10 regression

  • \eNTK(\Xs, \Xs) on CIFAR-10: 1.8 terabytes of memory
  • \pNTK(\Xs, \Xs) on CIFAR-10: 18 gigabytes of memory
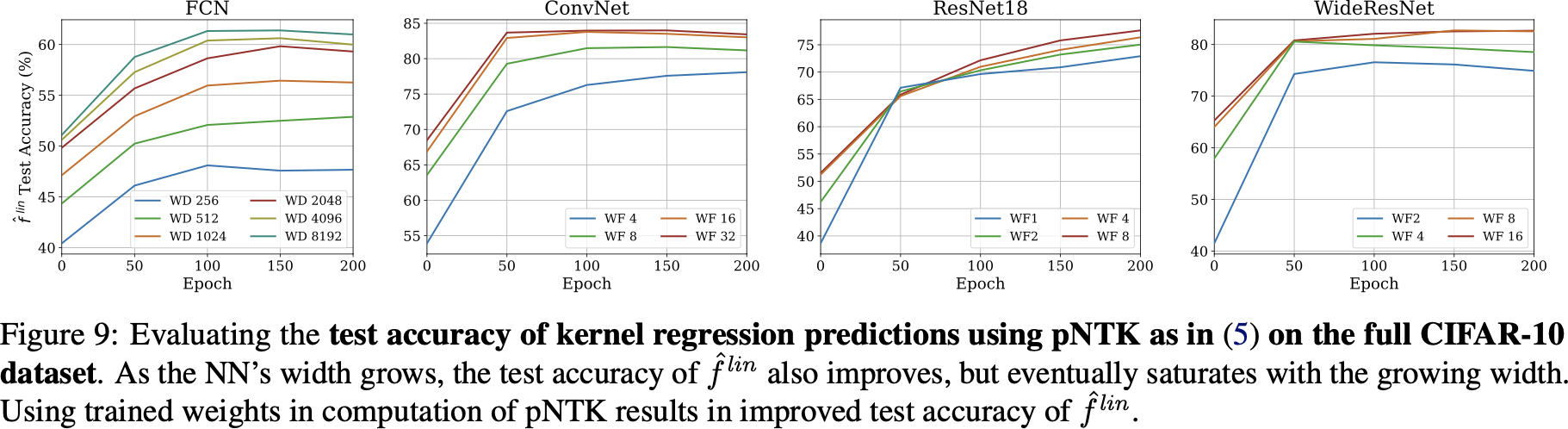
  • Worse than infinite NTK for FCN/ConvNet (where they can be computed, if you try hard)
  • Way worse than SGD

Recap

eNTK is a good tool for intuitive understanding of the learning process

Ren, Guo, S.
Better Supervisory Signals by Observing Learning Paths
Ren, Guo, Bae, S.
How to prepare your task head for finetuning

eNTK is practically very effective at “lookahead” for active learning

Mohamadi*, Bae*, S.
Making Look-Ahead Active Learning Strategies Feasible with Neural Tangent Kernels

You should probably use pNTK instead of eNTK for high-dim output problems:

Mohamadi, Bae, S.
A Fast, Well-Founded Approximation to the Empirical Neural Tangent Kernel